
【題目】定義:若兩條拋物線在x軸上經過兩個相同點,那么我們稱這兩條拋物線是“同交點拋物線”,在x軸上經過的兩個相同點稱為“同交點”,已知拋物線y=x2+bx+c經過(﹣2,0)、(﹣4,0),且一條與它是“同交點拋物線”的拋物線y=ax2+ex+f經過點(﹣3,3).
(1)求b、c及a的值;
(2)已知拋物線y=﹣x2+2x+3與拋物線yn=![]() x2﹣
x2﹣![]() x﹣n(n為正整數)
x﹣n(n為正整數)
①拋物線y和拋物線yn是不是“同交點拋物線”?若是,請求出它們的“同交點”,并寫出它們一條相同的圖像性質;若不是,請說明理由.
②當直線y=![]() x+m與拋物線y、yn,相交共有4個交點時,求m的取值范圍.
x+m與拋物線y、yn,相交共有4個交點時,求m的取值范圍.
③若直線y=k(k<0)與拋物線y=﹣x2+2x+3與拋物線yn =![]() x2﹣
x2﹣![]() x﹣n (n為正整數)共有4個交點,從左至右依次標記為點A、點B、點C、點D,當AB=BC=CD時,求出k、n之間的關系式
x﹣n (n為正整數)共有4個交點,從左至右依次標記為點A、點B、點C、點D,當AB=BC=CD時,求出k、n之間的關系式
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①是“同交點拋物線”,“同交點”為:(–1,0)、(3,0),它們圖形共同性質有:對稱軸同為直線
;(2)①是“同交點拋物線”,“同交點”為:(–1,0)、(3,0),它們圖形共同性質有:對稱軸同為直線![]() ;②
;②![]() ,且
,且![]() ,
,![]() ;③
;③![]()
【解析】
(1)將(–2,0)、( –4,0)代入![]() ,即可求得b、c的值,設“同交點拋物線”的解析式為
,即可求得b、c的值,設“同交點拋物線”的解析式為![]() ,將(–3,3)代入即可求得
,將(–3,3)代入即可求得![]() 的值;
的值;
(2)①令![]() 和
和![]() ,分別求得與
,分別求得與![]() 軸的交點坐標,即可作出判斷;
軸的交點坐標,即可作出判斷;
②先求得直線![]() 與拋物線
與拋物線![]() 或拋物線
或拋物線![]() 只有一個交點時
只有一個交點時![]() 的值,除去直線
的值,除去直線![]() 經過“同交點”時的
經過“同交點”時的![]() 的值,即可求解;
的值,即可求解;
③由![]() 和
和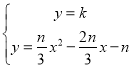 利用根與系數的關系求得
利用根與系數的關系求得![]() 和
和![]() 的值,再根據
的值,再根據![]() ,得到
,得到![]() 即可求得答案.
即可求得答案.
(1) ∵拋物線![]() 經過(–2,0)、( –4,0),則代入得:
經過(–2,0)、( –4,0),則代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
設“同交點拋物線”的解析式為![]() ,
,
將(–3,3)代入得:![]() ,
,
解得:![]() ,
,
故答案為:![]() ,
,![]() ,
,![]() ;
;
(2)①令![]() ,則
,則![]() ,
,
解得:![]() ,
,
∴拋物線![]() 與
與![]() 軸的交點坐標為:(–1,0)、(3,0),
軸的交點坐標為:(–1,0)、(3,0),
令![]() ,則
,則![]()
![]()
![]()
![]() ,
,
解得:![]() ,
,
∴拋物線![]() 與
與![]() 軸的交點坐標為:(–1,0)、(3,0),
軸的交點坐標為:(–1,0)、(3,0),
∴拋物線![]() 和拋物線
和拋物線![]() 是“同交點拋物線”,
是“同交點拋物線”,
它們圖形共同性質:對稱軸同為直線![]() ;
;
②當直線![]() 與拋物線y相交只有1個交點時,
與拋物線y相交只有1個交點時,
由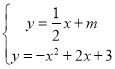 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
拋物線![]() 的頂點坐標為(1,
的頂點坐標為(1,![]() ),其中
),其中![]() 為正整數,
為正整數,
因為隨著![]() 的增大,
的增大,![]() 的頂點縱坐標減小,所以當直線
的頂點縱坐標減小,所以當直線![]() 與拋物線
與拋物線![]() 中
中![]() 時的拋物線相交只有1個交點時,
時的拋物線相交只有1個交點時,
由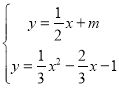 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
如圖所示:
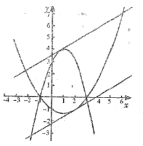
當直線![]() 經過“同交點”時與兩拋物線只有三個交點,
經過“同交點”時與兩拋物線只有三個交點,
把“同交點”(–1,0)代入![]() 得:
得:![]() ,
,
把“同交點” (3,0)代入![]() 得:
得:![]() ,
,
∴當直線![]() 與拋物線
與拋物線![]() 、
、![]() 有4個交點時,m的取值范圍為:
有4個交點時,m的取值范圍為:
![]() ,且
,且![]() ,
,![]() ;
;
③設直線![]() 分別與拋物線
分別與拋物線![]() 和拋物線
和拋物線![]() 相交于A、D、B、C,如圖:
相交于A、D、B、C,如圖:
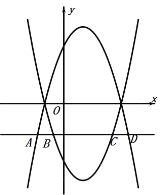
由![]() ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
由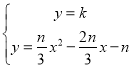 ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() .
.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3![]() ,BC=12,E為AD中點,F為AB上一點,將△AEF沿EF折疊后,點A恰好落到CF上的點G處,則折痕EF的長是_____.
,BC=12,E為AD中點,F為AB上一點,將△AEF沿EF折疊后,點A恰好落到CF上的點G處,則折痕EF的長是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
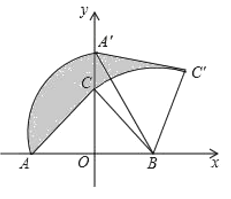
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中點O為坐標原點,AB所在直線為x軸建立的平面直角坐標系中,將△ABC繞點B順時針旋轉,使點A旋轉至y軸的正半軸上的點A'處,若AO=OB=2,則圖中陰影部分面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一次函數ymxn與反比例函數y![]() 同時經過點P(x,y)則稱二次函數ymx2nxk為一次函數與反比例函數的“共享函數”,稱點P為共享點.
同時經過點P(x,y)則稱二次函數ymx2nxk為一次函數與反比例函數的“共享函數”,稱點P為共享點.
(1)判斷y2x1與y![]() 是否存在“共享函數”,如果存在,請求出“共享點”.如果不存在,請說明理由;
是否存在“共享函數”,如果存在,請求出“共享點”.如果不存在,請說明理由;
(2)已知:整數m,n,t滿足條件t<n<8m,并且一次函數y=(1+n)x+2m+2與反比例函數y![]() 存在“共享函數”y=(m+t)x2+(10mt)x2020,求m的值.
存在“共享函數”y=(m+t)x2+(10mt)x2020,求m的值.
(3)若一次函數yxm和反比例函數y![]() 在自變量x的值滿足mxm6的情況下,其“共享函數”的最小值為3,求其“共享函數”的解析式.
在自變量x的值滿足mxm6的情況下,其“共享函數”的最小值為3,求其“共享函數”的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年,隨著電子產品的廣泛應用,學生的近視發生率出現低齡化趨勢,引起了相關部門的重視.某區為了了解在校學生的近視低齡化情況,對本區7-18歲在校近視學生進行了簡單的隨機抽樣調查,并繪制了以下兩幅不完整的統計圖.

請根據圖中信息,回答下列問題:
(1)這次抽樣調查中共調查了近視學生 人;
(2)請補全條形統計圖;
(3)扇形統計圖中10-12歲部分的圓心角的度數是 ;
(4)據統計,該區7-18歲在校學生近視人數約為10萬,請估計其中7-12歲的近視學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某數學活動小組為測量學校旗桿AB的高度,沿旗桿正前方![]() 米處的點C出發,沿斜面坡度
米處的點C出發,沿斜面坡度![]() 的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB//DE.求旗桿AB的高度.(參考數據:sin37°≈
的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB//DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .計算結果保留根號)
.計算結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB為⊙O的直徑,C為⊙O上一點,BG與⊙O相切于點B,交AC的延長線于點D(點D在線段BG上),AC = 8,tan∠BDC =![]()
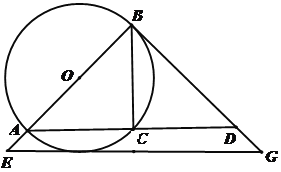
(1)求⊙O的直徑;
(2)當DG=![]() 時,過G作
時,過G作![]() ,交BA的延長線于點E,說明EG與⊙O相切.
,交BA的延長線于點E,說明EG與⊙O相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
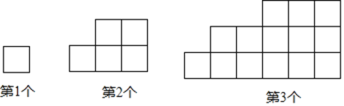
【題目】下列圖形都是由大小相同的小正方形按一定規律組成的,其中第1個圖形的周長為4,第2個圖形的周長為10,第3個圖形的周長為18,…,按此規律排列,回答下列問題:
(1)第5個圖形的周長為 ;
(2)第![]() 個圖形的周長為 ;
個圖形的周長為 ;
(3)若第![]() 個圖形的周長為180,則
個圖形的周長為180,則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
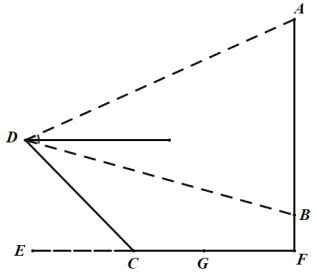
【題目】如圖,為測量瀑布![]() 的高度,測量人員在瀑布對面山上的
的高度,測量人員在瀑布對面山上的![]() 點處測得瀑布頂端
點處測得瀑布頂端![]() 點的仰角是
點的仰角是![]() ,測得瀑布底端
,測得瀑布底端![]() 點的俯角是
點的俯角是![]() ,
,![]() 與水平面垂直.又在瀑布下的水平面測得
與水平面垂直.又在瀑布下的水平面測得![]() ,
,![]() (注:
(注:![]() 、
、![]() 、
、![]() 三點在同一直線上,
三點在同一直線上,![]() 于點
于點![]() ),斜坡
),斜坡![]() ,坡角
,坡角![]() ,那么瀑布
,那么瀑布![]() 的高度約為( ).(精確到
的高度約為( ).(精確到![]() ,參考數據:
,參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.![]()
![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com