
【題目】如圖,在平面直角坐標(biāo)系中,長(zhǎng)方形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),動(dòng)點(diǎn)
的中點(diǎn),動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),以每秒
點(diǎn)出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度,沿著
個(gè)單位長(zhǎng)度的速度,沿著![]() 運(yùn)動(dòng),設(shè)點(diǎn)
運(yùn)動(dòng),設(shè)點(diǎn)![]() 運(yùn)動(dòng)的時(shí)間為
運(yùn)動(dòng)的時(shí)間為![]() 秒(
秒(![]() ).
).
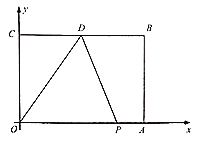
(1)點(diǎn)![]() 的坐標(biāo)是______;
的坐標(biāo)是______;
(2)當(dāng)點(diǎn)![]() 在
在![]() 上運(yùn)動(dòng)時(shí),點(diǎn)
上運(yùn)動(dòng)時(shí),點(diǎn)![]() 的坐標(biāo)是______(用
的坐標(biāo)是______(用![]() 表示);
表示);
(3)求![]() 的面積
的面積![]() 與
與![]() 之間的函數(shù)表達(dá)式,并寫(xiě)出對(duì)應(yīng)自變量
之間的函數(shù)表達(dá)式,并寫(xiě)出對(duì)應(yīng)自變量![]() 的取值范圍.
的取值范圍.
【答案】(1)(3,4);(2)(6,t-6)(3)
【解析】
(1)根據(jù)長(zhǎng)方形的性質(zhì)和A、B的坐標(biāo),即可求出OA=BC=6,OC=AB=4,再根據(jù)中點(diǎn)的定義即可求出點(diǎn)D的坐標(biāo);
(2)畫(huà)出圖形,易知:點(diǎn)P的橫坐標(biāo)為6,然后根據(jù)路程=速度×?xí)r間,即可求出點(diǎn)P的運(yùn)動(dòng)路程,從而求出AP的長(zhǎng),即可得出點(diǎn)P的坐標(biāo);
(3)分別求出點(diǎn)P到達(dá)A、B、D三點(diǎn)所需時(shí)間,然后根據(jù)點(diǎn)P運(yùn)動(dòng)到OA、AB、BD分類(lèi)討論,并寫(xiě)出t對(duì)應(yīng)的取值范圍,然后畫(huà)出圖形,利用面積公式即可求出各種情況下![]() 與
與![]() 之間的函數(shù)表達(dá)式.
之間的函數(shù)表達(dá)式.
解:(1)∵長(zhǎng)方形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]() ,
,
∴OA=BC=6,OC=AB=4,BA⊥x軸,BC⊥y軸
∵![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
∴CD=BD=![]() BC=3
BC=3
∴點(diǎn)D的坐標(biāo)為(3,4)
故答案為:(3,4);
(2)當(dāng)點(diǎn)![]() 在
在![]() 上運(yùn)動(dòng)時(shí),如下圖所示
上運(yùn)動(dòng)時(shí),如下圖所示

易知:點(diǎn)P的橫坐標(biāo)為6,
∵動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),以每秒
點(diǎn)出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度,時(shí)間為t
個(gè)單位長(zhǎng)度的速度,時(shí)間為t
∴點(diǎn)P運(yùn)動(dòng)的路程OA+AP=t
∴AP=t-6
∴點(diǎn)P的坐標(biāo)為(6,t-6)
故答案為:(6,t-6);
(3)根據(jù)點(diǎn)P的速度可知:點(diǎn)P到達(dá)A點(diǎn)所需時(shí)間為OA÷1=6s
點(diǎn)P到達(dá)B點(diǎn)所需時(shí)間為(OA+AB)÷1=10s
點(diǎn)P到達(dá)D點(diǎn)所需時(shí)間為(OA+AB+BD)÷1=13s
①當(dāng)點(diǎn)P在OA上運(yùn)動(dòng)時(shí),此時(shí)![]() ,過(guò)點(diǎn)D作DE⊥x軸于E
,過(guò)點(diǎn)D作DE⊥x軸于E
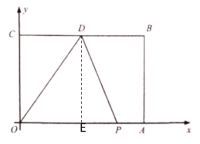
∴DE=4
∵動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),以每秒
點(diǎn)出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度,
個(gè)單位長(zhǎng)度的速度,
∴OP=t
∴![]() ;
;
②當(dāng)點(diǎn)P在AB上運(yùn)動(dòng)時(shí),此時(shí)![]() ,
,
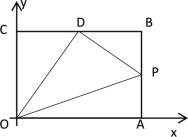
由(2)知AP=t-6
∴BP=AB-AP=10-t
∴![]()
=![]()
=![]()
=![]() ;
;
③當(dāng)點(diǎn)P在BD上運(yùn)動(dòng)時(shí),此時(shí)![]() ,
,
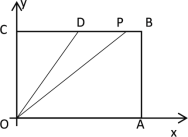
∵動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),以每秒
點(diǎn)出發(fā),以每秒![]() 個(gè)單位長(zhǎng)度的速度,時(shí)間為t
個(gè)單位長(zhǎng)度的速度,時(shí)間為t
∴點(diǎn)P運(yùn)動(dòng)的路程OA+AB+BP=t
∴BP=t-OA-AB=t-10
∴DP=BD-BP=13-t
![]()
=![]()
=![]()
綜上所述:


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
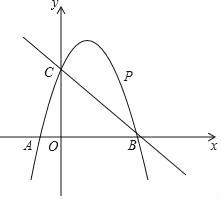
【題目】如圖,已知二次函數(shù)y=ax2+2x+c的圖象經(jīng)過(guò)點(diǎn)C(0,3),與x軸分別交于點(diǎn)A,點(diǎn)B(3,0).點(diǎn)P是直線(xiàn)BC上方的拋物線(xiàn)上一動(dòng)點(diǎn).
(1)求二次函數(shù)y=ax2+2x+c的表達(dá)式;
(2)連接PO,PC,并把△POC沿y軸翻折,得到四邊形POP′C.若四邊形POP′C為菱形,請(qǐng)求出此時(shí)點(diǎn)P的坐標(biāo);
(3)當(dāng)點(diǎn)P運(yùn)動(dòng)到什么位置時(shí),四邊形ACPB的面積最大?求出此時(shí)P點(diǎn)的坐標(biāo)和四邊形ACPB的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(綜合與實(shí)踐
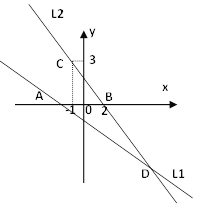
如圖,直線(xiàn)![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為![]() ,且
,且![]() 與
與![]() 軸交于點(diǎn)A,直線(xiàn)
軸交于點(diǎn)A,直線(xiàn)![]() 經(jīng)過(guò)點(diǎn)B(2,0),C(-1,3),直線(xiàn)
經(jīng)過(guò)點(diǎn)B(2,0),C(-1,3),直線(xiàn)![]() 與
與![]() 交于點(diǎn)D.
交于點(diǎn)D.
(1)求直線(xiàn)![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求△ABD的面積.
(3)點(diǎn)P是![]() 軸上一動(dòng)點(diǎn),問(wèn)是否存在一點(diǎn)P,恰好使△ADP為直角三角形?若存在,直接寫(xiě)出點(diǎn)P的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
軸上一動(dòng)點(diǎn),問(wèn)是否存在一點(diǎn)P,恰好使△ADP為直角三角形?若存在,直接寫(xiě)出點(diǎn)P的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,已知直線(xiàn)![]() 的同側(cè)有兩個(gè)點(diǎn)
的同側(cè)有兩個(gè)點(diǎn)![]() 、
、![]() ,在直線(xiàn)
,在直線(xiàn)![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使
,使![]() 點(diǎn)到
點(diǎn)到![]() 、
、![]() 兩點(diǎn)的距離之和最短的問(wèn)題,可以通過(guò)軸對(duì)稱(chēng)來(lái)確定,即作出其中一點(diǎn)關(guān)于直線(xiàn)
兩點(diǎn)的距離之和最短的問(wèn)題,可以通過(guò)軸對(duì)稱(chēng)來(lái)確定,即作出其中一點(diǎn)關(guān)于直線(xiàn)![]() 的對(duì)稱(chēng)點(diǎn),對(duì)稱(chēng)點(diǎn)與另一點(diǎn)的連線(xiàn)與直線(xiàn)
的對(duì)稱(chēng)點(diǎn),對(duì)稱(chēng)點(diǎn)與另一點(diǎn)的連線(xiàn)與直線(xiàn)![]() 的交點(diǎn)就是所要找的點(diǎn),通過(guò)這種方法可以求解很多問(wèn)題.
的交點(diǎn)就是所要找的點(diǎn),通過(guò)這種方法可以求解很多問(wèn)題.
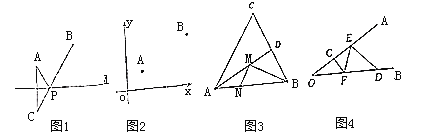
(1)如圖2,在平面直角坐標(biāo)系內(nèi),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)![]() 在
在![]() 軸上,求
軸上,求![]() 的最小值;
的最小值;
(2)如圖3,在銳角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分線(xiàn)交
的角平分線(xiàn)交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 、
、![]() 分別是
分別是![]() 和
和![]() 上的動(dòng)點(diǎn),則
上的動(dòng)點(diǎn),則![]() 的最小值為______.
的最小值為______.
(3)如圖4,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是射線(xiàn)
分別是射線(xiàn)![]() ,
,![]() 上的動(dòng)點(diǎn),則
上的動(dòng)點(diǎn),則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某民俗旅游村為接待游客住宿需要,開(kāi)設(shè)了有![]() 張床位的旅館,當(dāng)每張床位每天收費(fèi)
張床位的旅館,當(dāng)每張床位每天收費(fèi)![]() 元時(shí),床位可全部租出.若每張床位每天收費(fèi)提高
元時(shí),床位可全部租出.若每張床位每天收費(fèi)提高![]() 元,則相應(yīng)的減少了
元,則相應(yīng)的減少了![]() 張床位租出.如果每張床位每天以
張床位租出.如果每張床位每天以![]() 元為單位提高收費(fèi),為使租出的床位少且租金高,那么每張床位每天最合適的收費(fèi)是( )
元為單位提高收費(fèi),為使租出的床位少且租金高,那么每張床位每天最合適的收費(fèi)是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
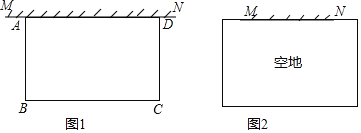
【題目】空地上有一段長(zhǎng)為a米的舊墻MN,某人利用舊墻和木欄圍成一個(gè)矩形菜園ABCD,已知木欄總長(zhǎng)為100米.
(1)已知a=20,矩形菜園的一邊靠墻,另三邊一共用了100米木欄,且圍成的矩形菜園面積為450平方米.如圖1,求所利用舊墻AD的長(zhǎng);
(2)已知0<α<50,且空地足夠大,如圖2.請(qǐng)你合理利用舊墻及所給木欄設(shè)計(jì)一個(gè)方案,使得所圍成的矩形菜園ABCD的面積最大,并求面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,已知![]() 、
、![]() ,
,![]() 為一次函數(shù)
為一次函數(shù)![]() 的圖像上一點(diǎn),且
的圖像上一點(diǎn),且![]() ,則點(diǎn)
,則點(diǎn)![]() 的坐標(biāo)為_____________________.
的坐標(biāo)為_____________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
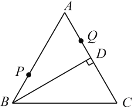
【題目】如圖,等邊△![]() 中,
中,![]() 于
于![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的兩個(gè)定點(diǎn)且
上的兩個(gè)定點(diǎn)且![]() ,在
,在![]() 上有一動(dòng)點(diǎn)
上有一動(dòng)點(diǎn)![]() 使
使![]() 最短,則
最短,則![]() 的最小值為_____
的最小值為_____![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】勾股定理是人類(lèi)最偉大的科學(xué)發(fā)現(xiàn)之一,在我國(guó)古算書(shū)《周髀算經(jīng)》中早有記載.如圖1,以直角三角形的各邊為邊分別向外作正方形,再把較小的兩張正方形紙片按圖2的方式放置在最大正方形內(nèi).若知道圖中陰影部分的面積,則一定能求出( )

A.直角三角形的面積
B.最大正方形的面積
C.較小兩個(gè)正方形重疊部分的面積
D.最大正方形與直角三角形的面積和
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com