
【題目】如圖,已知△ABC中,AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,連接BD,CE交于點F,BD交AE于M. 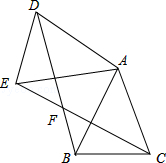
(1)求證:△AEC≌△ADB;
(2)若BC=2,∠BAC=30°,當四邊形ADFC是菱形時,求BF的長.
【答案】
(1)解:由旋轉的性質得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠DAB,
在△AEC和△ADB中,
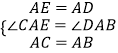 ,
,
∴△AEC≌△ADB(SAS)
(2)解:如圖,過點B作BG⊥EC于點G,
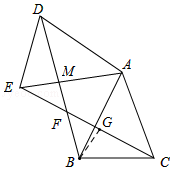
∵∠BAC=30°,AB=AC,
∴∠ABC=∠ACB=75°.
∵當四邊形ADFC是菱形時,AC∥DF,
∴∠FBA=∠BAC=30°,
∵AB=AD,
∴∠ADB=∠ABD=30°,
∴∠ACE=∠ADB=30°,
∴∠FCB=45°.
∵BG⊥EC,
∴∠GBC=45°,
∴BG=GC=BCsin45°= ![]() ×2=
×2= ![]() ,
,
∵∠ABC=75°,∠ABD=30°,∠FCB=45°
∴∠BFC=180°﹣75°﹣45°﹣30°=30°,
∴BF=2BG=2 ![]()
【解析】(1)根據旋轉的性質得:△ABC≌△ADE,且AB=AC,進而得到∠CAE=∠DAB,再根據SAS即可判定△AEC≌△ADB;(2)過點B作BG⊥EC于點G,根據四邊形ADFC是菱形,以及等腰三角形的性質,得出∠FCB=45°,求得BG=GC=BCsin45°= ![]() ×2=
×2= ![]() ,再根據∠BFC=30°,即可得到BF=2BG.
,再根據∠BFC=30°,即可得到BF=2BG.
【考點精析】利用等腰直角三角形和含30度角的直角三角形對題目進行判斷即可得到答案,需要熟知等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°;在直角三角形中,如果一個銳角等于30°,那么它所對的直角邊等于斜邊的一半.


科目:初中數學 來源: 題型:
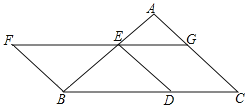
【題目】如圖,以BC為底邊的等腰![]() ,點D,E,G分別在BC,AB,AC上,且
,點D,E,G分別在BC,AB,AC上,且![]() ,
,![]() ,延長GE至點F,使得
,延長GE至點F,使得![]() .
.
![]() 求證:四邊形BDEF為平行四邊形;
求證:四邊形BDEF為平行四邊形;
![]() 當
當![]() ,
,![]() 時,聯結DF,求線段DF的長.
時,聯結DF,求線段DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校去年在某商場購買甲、乙兩種不同足球,購買甲種足球共花費2400元,購買乙種足球共花費1600元,購買甲種足球數量是購買乙種足球數量的2倍.且購買一個乙種足球比購買一個甲種足球多花20元.
(1)求購買一個甲種足球、一個乙種足球各需多少元;
(2)今年學校為編排“足球操”,決定再次購買甲、乙兩種足球共50個.如果兩種足球的單價沒有改變,而此次購買甲、乙兩種足球的總費用不超過3500元,那么這所學校最少可購買多少個甲種足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次考試中,某班級的數學成績統計圖如下.下列說法錯誤的是( )

A. 得分在70~80分之間的人數最多
B. 該班的總人數為40
C. 得分在90~100分之間的人數最少
D. 及格(≥60分)人數是26
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區在實施居民用水額定管理前,對居民生活用水情況進行了調查,下表是通過簡單隨機抽樣獲得的50個家庭去年月平均用水量(單位:噸),并將調查數據進行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
頻數分布表
分組 | 劃記 | 頻數 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合計 | 50 |
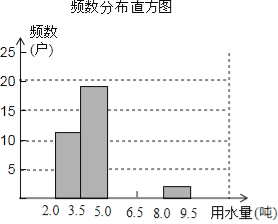
(1)把上面頻數分布表和頻數分布直方圖補充完整;
(2)從直方圖中你能得到什么信息?(寫出兩條即可);
(3)為了鼓勵節約用水,要確定一個用水量的標準,超出這個標準的部分按1.5倍價格收費,若要使60%的家庭收費不受影響,你覺得家庭月均用水量應該定為多少?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中:![]() 有公共頂點和一條公共邊的兩個角一定是鄰補角;
有公共頂點和一條公共邊的兩個角一定是鄰補角;![]() 垂線段最短;
垂線段最短;![]() 經過直線外一點,有且只有一條直線與這條直線平行;
經過直線外一點,有且只有一條直線與這條直線平行;![]() 相等的角是對頂角;
相等的角是對頂角;![]() 等角的余角相等,其中假命題的個數是
等角的余角相等,其中假命題的個數是![]()
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題
情景:

試根據圖中的信息,解答下列問題:
(1)購買6根跳繩需___________元,購買12根跳繩需_____________元.
(2)小紅比小明多買2根,付款時小紅反而比小明少5元,你認為有這種可能嗎?若有,請求出小紅購買跳繩的根數;若沒有,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com