
【題目】在平面直角坐標系xOy中,對于點P(x,y)和Q(x,y′),給出如下定義:如果y′= ![]() ,那么稱點Q為點P的“關聯點”.例如:點(5,6)的“關聯點”為點(5,6),點(﹣5,6)的“關聯點”為點(﹣5,﹣6).
,那么稱點Q為點P的“關聯點”.例如:點(5,6)的“關聯點”為點(5,6),點(﹣5,6)的“關聯點”為點(﹣5,﹣6).
(1)如果點A(3,﹣1),B(﹣1,3)的“關聯點”中有一個在函數y= ![]() 的圖象上,那么這個點是(填“點A”或“點B”).
的圖象上,那么這個點是(填“點A”或“點B”).
(2)如果點N*(m+1,2)是一次函數y=x+3圖象上點N的“關聯點”,求點N的坐標.
(3)如果點P在函數y=﹣x2+4(﹣2<x≤a)的圖象上,其“關聯點”Q的縱坐標y′的取值范圍是﹣4<y′≤4,那么實數a的取值范圍.
【答案】
(1)B
(2)
解:如果點N*(m+1,2)是一次函數y=x+3圖象上,
點N*(﹣1,2)的“關聯點”(﹣1,﹣2),
點N的坐標是(﹣1,﹣2);
(3)
解:如果點P在函數y=﹣x2+4(﹣2<x≤a)的圖象上,
當﹣2<x≤0時,0<y≤4,即﹣2<a≤0;
當x>0時,y=y′,即﹣4<y≤4,
﹣x2+4>﹣4,解得x<2 ![]() ,即0<a<2
,即0<a<2 ![]() .
.
綜上所述:“關聯點”Q的縱坐標y′的取值范圍是﹣4<y′≤4,那么實數a的取值范圍是﹣2<a<2 ![]() .
.
【解析】解:(1)如果點A(3,﹣1)的關聯點為(3,﹣1);B(﹣1,3)的“關聯點”為(﹣1,﹣3),一個在函數y= ![]() 的圖象上,那么這個點是 B;
的圖象上,那么這個點是 B;
所以答案是:B;


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+2x+3與x軸交于A,B兩點,與y軸交于點C,點D為拋物線的頂點,請解決下列問題.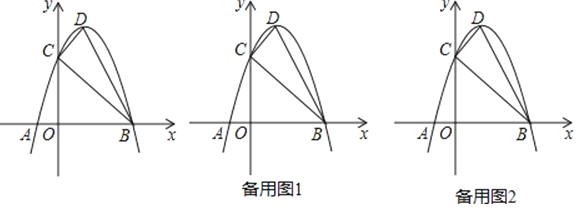
(1)填空:點C的坐標為 點D的坐標為 ;
(2)設點P的坐標為(a,0),當|PD﹣PC|最大時,求α的值并在圖中標出點P的位置;
(3)在(2)的條件下,將△BCP沿x軸的正方向平移得到△B′C′P′,設點C對應點C′的橫坐標為t(其中0<t<6),在運動過程中△B′C′P′與△BCD重疊部分的面積為S,求S與t之間的關系式,并直接寫出當t為何值時S最大,最大值為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現正是閩北特產楊梅熱銷的季節,某水果零售商店分兩批次從批發市場共購進楊梅40箱,已知第一、二次進貨價分別為每箱50元、40元,且第二次比第一次多付款700元.
(1)設第一、二次購進楊梅的箱數分別為a箱、b箱,求a,b的值;
(2)若商店對這40箱楊梅先按每箱60元銷售了x箱,其余的按每箱35元全部售完.
①求商店銷售完全部楊梅所獲利潤y(元)與x(箱)之間的函數關系式;
②當x的值至少為多少時,商店才不會虧本.
(注:按整箱出售,利潤=銷售總收入﹣進貨總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,點M、N分別在AB、AD邊上,若AM:MB=AN:ND=1:2.則 cos∠MCN= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為1的小正方形組成的正方形網格中建立如圖片所示的平面直角坐標系,已知格點三角形ABC(三角形的三個頂點都在小正方形上)
(1)畫出△ABC關于直線l:x=﹣1的對稱三角形△A1B1C1;并寫出A1、B1、C1的坐標.
(2)在直線x=﹣l上找一點D,使BD+CD最小,滿足條件的D點為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在9×9的正方形網格中,△ABC三個頂點在格點上,每個小正方形的邊長為1.
(1)建立適當的平面直角坐標系后,若點A的坐標為(1,1),點C的坐標為(4,2),畫出平面直角坐標系并寫出點B的坐標;
(2)直線l經過點A且與y軸平行,寫出點B、C關于直線l對稱點B1、C1的坐標;
(3)直接寫出BC上一點P(a,b)關于直線l對稱點P1的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次初中生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題: 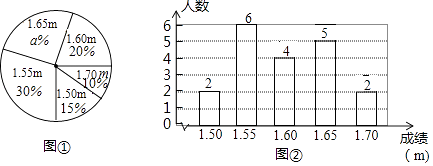
(1)①中a的值為;
(2)統計的這組初賽成績數據的平均數、眾數和中位數(結果保留小數點后兩位);
(3)據這組初賽成績,由高到低確定7人進入復賽,請直接寫出初賽成績為1.60m的運動員能否進入復賽.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園安全”受到全社會的廣泛關注,東營市某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了如圖兩幅尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題: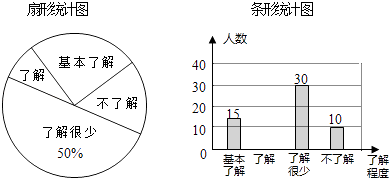
(1)接受問卷調查的學生共有 人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為 ;
(2)請補全條形統計圖;
(3)若該中學共有學生900人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數;
(4)若從對校園安全知識達到了“了解”程度的3個女生和2個男生中隨機抽取2人參加校園安全知識競賽,請用樹狀圖或列表法求出恰好抽到1個男生和1個女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
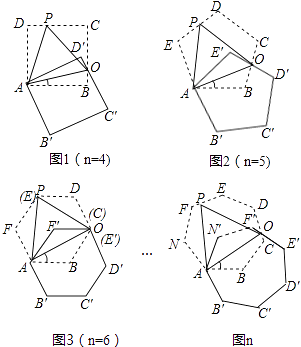
【題目】如圖,在正n邊形(n為整數,且n≥4)繞點A順時針旋轉60°后,發現旋轉前后兩圖形有另一交點O,連接AO,我們稱AO為“疊弦”;再將“疊弦”AO所在的直線繞點A逆時針旋轉60°后,交旋轉前的圖形于點P,連接PO,我們稱∠OAB為正n邊形的“疊弦角”,△AOP為“疊弦三角形”.以下說法,正確的是 . (填番號)
①在圖1中,△AOB≌△AOD';
②在圖2中,正五邊形的“疊弦角”的度數為360°;
③“疊弦三角形”不一定都是等邊三角形; ④正n邊形的“疊弦角”的度數為60°﹣ ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com