
【題目】如圖,以直角三角形a、b、c為邊,向外作等邊三角形,半圓,等腰直角三角形和正方形,上述四種情況的面積關系滿足S1+S2=S3圖形個數有( ) 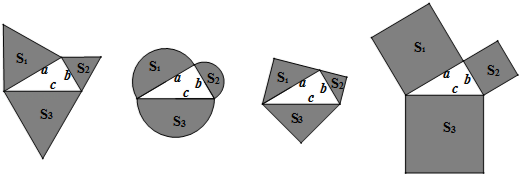
A.1
B.2
C.3
D.4
【答案】D
【解析】解:(1)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 , ∵a2+b2=c2 ,
c2 , ∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (2)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (3)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (4)S1=a2 , S2=b2 , S3=c2 ,
∵a2+b2=c2 ,
∴S1+S2=S3 .
綜上,可得
面積關系滿足S1+S2=S3圖形有4個.
故選:D.
根據直角三角形a、b、c為邊,應用勾股定理,可得a2+b2=c2 . (1)第一個圖形中,首先根據等邊三角形的面積的求法,表示出3個三角形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (2)第二個圖形中,首先根據圓的面積的求法,表示出3個半圓的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (3)第三個圖形中,首先根據等腰直角三角形的面積的求法,表示出3個等腰直角三角形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (4)第四個圖形中,首先根據正方形的面積的求法,表示出3個正方形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 .


科目:初中數學 來源: 題型:
【題目】如圖,一架2.5米長的梯子AB,斜靠在一豎直的墻AC上,這時梯足B到墻底端C的距離為0.7米,如果梯子的頂端沿墻下滑0.4米,那么梯足將向外移多少米? 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個性狀、大小相同的大長方形內放入四個如圖③的小長方形后得圖①、圖②,已知大長方形的長為a,則圖①陰影部分的周長與圖②陰影部分的周長的差是 . (用含a的代數式表示) 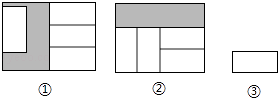
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在3×3的方格紙中,點A,B,C,D,E分別位于如圖所示的小正方形格點上.
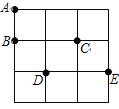
(1)在點A,B,C,D,E中任取四個點為頂點直接在圖上畫一個中心對稱的四邊形;
(2)從A,B,C三個點中先任取一個點,在余下的兩個點中再取一個點,將所取的這兩點與點D,E為頂點構成四邊形,求所得四邊形中面積為2的概率(用樹狀圖或列表法求解).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com