
【題目】斐波那契數(shù)列,又稱黃金分割數(shù)列.因數(shù)學(xué)家列昂納多·斐波那契以兔子繁殖為例子而引入,故又稱為“兔子數(shù)列”,指的是這樣一個(gè)數(shù)列:1、1、2、3、5、8、13、21、34、…..,在數(shù)學(xué)上,斐波那契數(shù)列以如下被遞推的方法定義:![]() ,
,![]() ,
,![]() .這種遞推方法適合研究生活中很多問(wèn)題.比如:一六八中學(xué)食堂一樓到二樓有15個(gè)臺(tái)階,某同學(xué)一步可以跨一個(gè)或者兩個(gè)臺(tái)階,則他到二樓就餐有( )種上樓方法.
.這種遞推方法適合研究生活中很多問(wèn)題.比如:一六八中學(xué)食堂一樓到二樓有15個(gè)臺(tái)階,某同學(xué)一步可以跨一個(gè)或者兩個(gè)臺(tái)階,則他到二樓就餐有( )種上樓方法.
A.377B.610C.987D.1597
【答案】C
【解析】
分析出![]() ,
,![]() ,
,![]() ,
,![]() ,進(jìn)而得到遞推關(guān)系
,進(jìn)而得到遞推關(guān)系![]() ,滿足斐波那契數(shù)列,列舉即可得到結(jié)果.
,滿足斐波那契數(shù)列,列舉即可得到結(jié)果.
由題意若只有一個(gè)臺(tái)階,則有![]() 種上樓方法;
種上樓方法;
若有兩個(gè)臺(tái)階,則有![]() 種上樓方法;
種上樓方法;
若有三個(gè)臺(tái)階,則有![]() 種上樓方法;
種上樓方法;
若有四個(gè)臺(tái)階,則有![]() 種上樓方法;
種上樓方法;
以此類推:
若要到達(dá)第n個(gè)臺(tái)階,前一步可能在第n-1個(gè)臺(tái)階上再跨一臺(tái)階上去,也可能是在第n-2個(gè)臺(tái)階上跨兩個(gè)臺(tái)階上去,
∴滿足![]() ,符合斐波那契數(shù)列的規(guī)律,由此規(guī)律列舉出前15項(xiàng):
,符合斐波那契數(shù)列的規(guī)律,由此規(guī)律列舉出前15項(xiàng):
1、2、3、5、8、13、21、34、55、89、144、233、377、610、987
∴有15個(gè)臺(tái)階,則他到二樓就餐有987種上樓方法.
故選:C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從某居民區(qū)隨機(jī)抽取10個(gè)家庭,獲得第![]() 個(gè)家庭的月收入
個(gè)家庭的月收入![]() (單位:千元)與月儲(chǔ)蓄
(單位:千元)與月儲(chǔ)蓄![]() (單位:千元)的數(shù)據(jù)資料,算得
(單位:千元)的數(shù)據(jù)資料,算得![]() ,
, ![]() ,
,
![]() ,
, ![]()
(1).求家庭的月儲(chǔ)蓄![]() 對(duì)月收入
對(duì)月收入![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2).判斷變量![]() 與
與![]() 之間的正相關(guān)還是負(fù)相關(guān);
之間的正相關(guān)還是負(fù)相關(guān);
(3).若該居民區(qū)某家庭月收入為7千元,預(yù)測(cè)該家庭的月儲(chǔ)蓄.
附:回歸直線的斜率和截距的最小二乘估計(jì)公式分別為

![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 是等邊三角形,四邊形ABCD是矩形,
是等邊三角形,四邊形ABCD是矩形,![]() ,F為棱PA上一點(diǎn),且
,F為棱PA上一點(diǎn),且![]() ,M為AD的中點(diǎn),四棱錐
,M為AD的中點(diǎn),四棱錐![]() 的體積為
的體積為![]() .
.
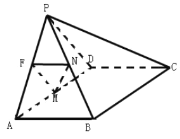
(1)若![]() ,N是PB的中點(diǎn),求證:平面
,N是PB的中點(diǎn),求證:平面![]() 平面PCD;
平面PCD;
(2)是否存在![]() ,使得平面FMB與平面PAD所成的二面角余弦的絕對(duì)值為
,使得平面FMB與平面PAD所成的二面角余弦的絕對(duì)值為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】長(zhǎng)沙某超市計(jì)劃按月訂購(gòu)一種冰激凌,每天進(jìn)貨量相同,進(jìn)貨成本為每桶5元,售價(jià)為每桶7元,未售出的冰激凌以每桶3元的價(jià)格當(dāng)天全部處理完畢.根據(jù)往年銷售經(jīng)驗(yàn),每天的需求量與當(dāng)天最高氣溫(單位:![]() )有關(guān),如果最高氣溫不低于
)有關(guān),如果最高氣溫不低于![]() ,需求量為600桶;如果最高氣溫(單位:
,需求量為600桶;如果最高氣溫(單位:![]() )位于區(qū)間
)位于區(qū)間![]() ,需求量為400桶;如果最高氣溫低于
,需求量為400桶;如果最高氣溫低于![]() ,需求量為200桶.為了確定今年九月份的訂購(gòu)計(jì)劃,統(tǒng)計(jì)了前三年九月份各天的最高氣溫?cái)?shù)據(jù),得下面的頻數(shù)分布表:
,需求量為200桶.為了確定今年九月份的訂購(gòu)計(jì)劃,統(tǒng)計(jì)了前三年九月份各天的最高氣溫?cái)?shù)據(jù),得下面的頻數(shù)分布表:
最高氣溫( |
|
|
|
|
|
|
天數(shù) | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區(qū)間的頻率代替最高氣溫位于該區(qū)間的概率.
(1)求九月份這種冰激凌一天的需求量![]() (單位:桶)的分布列;
(單位:桶)的分布列;
(2)設(shè)九月份一天銷售這種冰激凌的利潤(rùn)為![]() (單位:元),當(dāng)九月份這種冰激凌一天的進(jìn)貨量
(單位:元),當(dāng)九月份這種冰激凌一天的進(jìn)貨量![]() (單位:桶)為多少時(shí),
(單位:桶)為多少時(shí),![]() 的均值取得最大值?
的均值取得最大值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]()
(1)求![]() 的值;
的值;
(2)![]() 時(shí),求
時(shí),求![]() 的取值范圍;
的取值范圍;
(3)函數(shù)的性質(zhì)通常指的是函數(shù)的定義域、值域、單調(diào)性、周期性、奇偶性等,請(qǐng)你探究函數(shù)![]() 其中的三個(gè)性質(zhì)(直接寫(xiě)出結(jié)論即可)
其中的三個(gè)性質(zhì)(直接寫(xiě)出結(jié)論即可)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時(shí)的速度行駛1小時(shí),消耗10升汽油
D. 某城市機(jī)動(dòng)車最高限速80千米/小時(shí). 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2020年開(kāi)始,國(guó)家逐步推行全新的高考制度,新高考不再分文理科。某省采用![]() 模式,其中語(yǔ)文、數(shù)學(xué)、外語(yǔ)三科為必考科目,滿分各150分,另外考生還要依據(jù)想考取的高校及專業(yè)的要求,結(jié)合自己的興趣愛(ài)好等因素,在思想政治、歷史、地理、物理、化學(xué)、生物6門(mén)科目中自選3門(mén)參加考試(6選3),每科目滿分100分.為了應(yīng)對(duì)新高考,某學(xué)校從高一年級(jí)1000名學(xué)生(其中男生550人,女生450人)中,根據(jù)性別分層,采用分層抽樣的方法從中抽取100名學(xué)生進(jìn)行調(diào)查.
模式,其中語(yǔ)文、數(shù)學(xué)、外語(yǔ)三科為必考科目,滿分各150分,另外考生還要依據(jù)想考取的高校及專業(yè)的要求,結(jié)合自己的興趣愛(ài)好等因素,在思想政治、歷史、地理、物理、化學(xué)、生物6門(mén)科目中自選3門(mén)參加考試(6選3),每科目滿分100分.為了應(yīng)對(duì)新高考,某學(xué)校從高一年級(jí)1000名學(xué)生(其中男生550人,女生450人)中,根據(jù)性別分層,采用分層抽樣的方法從中抽取100名學(xué)生進(jìn)行調(diào)查.
(1)學(xué)校計(jì)劃在高一上學(xué)期開(kāi)設(shè)選修中的“物理”和“歷史”兩個(gè)科目,為了了解學(xué)生對(duì)這兩個(gè)科目的選課情況,對(duì)抽取到的100名學(xué)生進(jìn)行問(wèn)卷調(diào)查(假定每名學(xué)生在這兩個(gè)科目中必須選擇一個(gè)科目且只能選擇一個(gè)科目),如下表是根據(jù)調(diào)查結(jié)果得到的![]() 列聯(lián)表.請(qǐng)求出
列聯(lián)表.請(qǐng)求出![]() 和
和![]() ,并判斷是否有
,并判斷是否有![]() 的把握認(rèn)為選擇科目與性別有關(guān)?說(shuō)明你的理由;
的把握認(rèn)為選擇科目與性別有關(guān)?說(shuō)明你的理由;
選擇“物理” | 選擇“歷史” | 總計(jì) | |
男生 |
| 10 | |
女生 | 25 |
| |
總計(jì) |
(2)在抽取到的女生中按(1)中的選課情況進(jìn)行分層抽樣,從中抽出9名女生,再?gòu)倪@9名女生中隨機(jī)抽取4人,設(shè)這4人中選擇“歷史”的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
參考公式: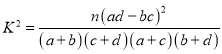
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() 分別為內(nèi)角
分別為內(nèi)角![]() 所對(duì)的邊,且滿足
所對(duì)的邊,且滿足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)現(xiàn)給出三個(gè)條件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
試從中選出兩個(gè)可以確定![]() 的條件,寫(xiě)出你的選擇并以此為依據(jù)求
的條件,寫(xiě)出你的選擇并以此為依據(jù)求![]() 的面積 (只需寫(xiě)出一個(gè)選定方案即可,選多種方案以第一種方案記分)
的面積 (只需寫(xiě)出一個(gè)選定方案即可,選多種方案以第一種方案記分)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com