
己知函數 .
.
(I)求 的極大值和極小值;
的極大值和極小值;
(II)當 時,
時, 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
(I) 的極大值為
的極大值為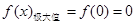 和
和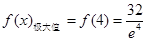 ;
; 的極小值為
的極小值為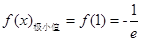 .(II)
.(II) 的取值范圍是
的取值范圍是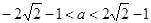 .
.
解析試題分析:(I) 易知函數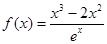 定義域為
定義域為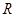 ,在
,在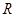 上討論
上討論 的極值先求導
的極值先求導 ,列出
,列出 的正負表,再根據函數的單調性和極值與倒數的關系即可求出極值.
的正負表,再根據函數的單調性和極值與倒數的關系即可求出極值.
(II) 本題是不等式恒成立求參數范圍問題,一般思路是化簡-分類討論,但本題中化簡后為 ,如果用
,如果用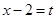 即
即 換元后為
換元后為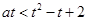 討論起來更簡單.分別討論?
討論起來更簡單.分別討論?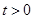 時,化簡為
時,化簡為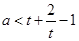 ;?
;?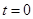 時,恒成立;?
時,恒成立;?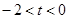 時化簡為
時化簡為 三種情況,運用均值不等式求出范圍即可.
三種情況,運用均值不等式求出范圍即可.
試題解析:(I) 函數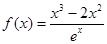 ,知定義域為
,知定義域為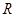 ,
, .
.
所以 的變化情況如下:
的變化情況如下: