
【題目】已知函數(shù)![]() ,
,![]() .
.![]() ,e為自然對數(shù)的底數(shù).
,e為自然對數(shù)的底數(shù).
(1)如果函數(shù)![]() 在(0,
在(0,![]() )上單調(diào)遞增,求m的取值范圍;
)上單調(diào)遞增,求m的取值范圍;
(2)若直線![]() 是函數(shù)
是函數(shù)![]() 圖象的一條切線,求實數(shù)k的值;
圖象的一條切線,求實數(shù)k的值;
(3)設(shè)![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() (2)1(3)見解析。
(2)1(3)見解析。
【解析】
(1)依題意h′(x)=ex﹣2mx≥0(0,+∞)上恒成立.即![]() 在(0,+∞)上恒成立.即求函數(shù)
在(0,+∞)上恒成立.即求函數(shù)![]() 的最小值即可;(2)設(shè)切點
的最小值即可;(2)設(shè)切點![]() ,則切線方程為則
,則切線方程為則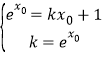 進(jìn)而得到
進(jìn)而得到![]() ,令
,令![]() 對函數(shù)求導(dǎo)得到函數(shù)的單調(diào)性和零點即可得到k值(3):要證
對函數(shù)求導(dǎo)得到函數(shù)的單調(diào)性和零點即可得到k值(3):要證![]() ,只要證
,只要證![]() ,兩邊同時除以
,兩邊同時除以![]() 令x2﹣x1=t,t>0,即證(t﹣2)et+t+2>0,利用
令x2﹣x1=t,t>0,即證(t﹣2)et+t+2>0,利用![]() =(t﹣2)et+t+2,(t>0)單調(diào)性即可證明
=(t﹣2)et+t+2,(t>0)單調(diào)性即可證明
:(1)![]() ,
,![]()
要使![]() 在
在![]() 上單調(diào)遞增,則
上單調(diào)遞增,則![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() ,∴
,∴![]() ,令
,令![]() ,
,![]()
當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,當(dāng)
單調(diào)遞減,當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞增
單調(diào)遞增
∴當(dāng)x=1時,![]() 有最小值為
有最小值為![]() ,∴
,∴![]()
(2)∵![]() ,∴
,∴![]() ,設(shè)切點為
,設(shè)切點為![]() ,則
,則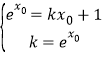
∴![]() ,令
,令![]() ,
,![]()
∴![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,當(dāng)k>1時,
單調(diào)遞減,當(dāng)k>1時,![]() ,
,![]() 單調(diào)遞增
單調(diào)遞增
∴k=1時,![]() ,∴
,∴![]() 時,k=1.∴實數(shù)k的值為1.
時,k=1.∴實數(shù)k的值為1.
(3)要證![]()
只要證![]() ,兩邊同時除以
,兩邊同時除以![]() 得:
得:
![]() ,令
,令![]() 得:
得:![]()
所以只要證:![]() ,令
,令![]()
∴![]() ,
,![]() ,∴
,∴![]()
即![]() ,∴原不等式成立.
,∴原不等式成立.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲乙兩個同學(xué)進(jìn)行定點投籃游戲,已知他們每一次投籃投中的概率均為![]() ,且各次投籃的結(jié)果互不影響.甲同學(xué)決定投5次,乙同學(xué)決定投中1次就停止,否則就繼續(xù)投下去,但投籃次數(shù)不超過5次.
,且各次投籃的結(jié)果互不影響.甲同學(xué)決定投5次,乙同學(xué)決定投中1次就停止,否則就繼續(xù)投下去,但投籃次數(shù)不超過5次.
(1)求甲同學(xué)至少有4次投中的概率;
(2)求乙同學(xué)投籃次數(shù)![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在棱長為1的正方體![]() 中,點
中,點![]() 分別是棱
分別是棱![]() 的中點,
的中點,![]() 是側(cè)面
是側(cè)面![]() 內(nèi)一點,若
內(nèi)一點,若![]() 平面
平面![]() ,則線段
,則線段![]() 長度的取值范圍是( )
長度的取值范圍是( )

A. B.
B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(.(12分)在一次購物抽獎活動中,假設(shè)某10張券中有一等獎獎券1張,可獲價值50元的獎品;有二等獎獎券3張,每張可獲價值10元的獎品;其余6張沒獎。某顧客從此10張獎券中任抽2張,求:
(1)該顧客中獎的概率;
(2)該顧客獲得的獎品總價值X(元)的概率分布列。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩名運動員進(jìn)行射擊訓(xùn)練,已知他們擊中的環(huán)數(shù)都穩(wěn)定在![]() 、
、![]() 、
、![]() 、
、![]() 環(huán),且每次射擊成績互不影響.根據(jù)以往的統(tǒng)計數(shù)據(jù),甲、乙射擊環(huán)數(shù)的頻率分布條形圖如下:
環(huán),且每次射擊成績互不影響.根據(jù)以往的統(tǒng)計數(shù)據(jù),甲、乙射擊環(huán)數(shù)的頻率分布條形圖如下:
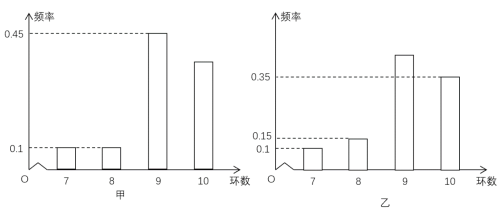
若將頻率視為概率,回答下列問題:
(1)甲、乙各射擊一次,求甲、乙同時擊中![]() 環(huán)的概率;
環(huán)的概率;
(2)求甲射擊一次,擊中![]() 環(huán)以上(含
環(huán)以上(含![]() 環(huán))的概率;
環(huán))的概率;
(3)甲射擊![]() 次,
次,![]() 表示這
表示這![]() 次射擊中擊中
次射擊中擊中![]() 環(huán)以上(含
環(huán)以上(含![]() 環(huán))的次數(shù),求
環(huán))的次數(shù),求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 為等差數(shù)列,
為等差數(shù)列,![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,若對一切
,若對一切![]() ,恒有
,恒有![]() ,則
,則![]() 能取到的最大整數(shù)是( )
能取到的最大整數(shù)是( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com