
【題目】設(shè)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若![]() 無零點,求實數(shù)
無零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() 有兩個相異零點
有兩個相異零點![]() ,
, ![]() ,求證:
,求證: ![]()
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】試題分析:(1)根據(jù)導(dǎo)數(shù)幾何意義得切線斜率為![]() ,再根據(jù)點斜式求切線方程(2)由于無零點,且函數(shù)恒有負值,所以函數(shù)最大值必小于零,根據(jù)導(dǎo)數(shù)可得函數(shù)最值,即得實數(shù)
,再根據(jù)點斜式求切線方程(2)由于無零點,且函數(shù)恒有負值,所以函數(shù)最大值必小于零,根據(jù)導(dǎo)數(shù)可得函數(shù)最值,即得實數(shù)![]() 的取值范圍;也可先變量分離,根據(jù)兩函數(shù)交點情況求實數(shù)
的取值范圍;也可先變量分離,根據(jù)兩函數(shù)交點情況求實數(shù)![]() 的取值范圍(3)利用分析法證不等式,要證
的取值范圍(3)利用分析法證不等式,要證![]() ,只要證
,只要證![]() ,根據(jù)零點條件可得
,根據(jù)零點條件可得![]() ,令
,令![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,
, ![]() ,利用導(dǎo)數(shù)可得
,利用導(dǎo)數(shù)可得![]() 單調(diào)性,即得
單調(diào)性,即得![]() ,逆推可得結(jié)論
,逆推可得結(jié)論
試題解析:(1)函數(shù)的定義域為![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() ,則切線方程為
,則切線方程為![]() ,
,
即![]() .
.
(2)①若![]() 時,則
時,則![]() ,
, ![]() 是區(qū)間
是區(qū)間![]() 上的增函數(shù),
上的增函數(shù),
∵![]() ,
, ![]() ,
,
∴![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 有唯一零點;
有唯一零點;
②若![]() ,
, ![]() 有唯一零點
有唯一零點![]() ;
;
③若![]() ,令
,令![]() ,得
,得![]() ,
,
在區(qū)間![]() 上,
上, ![]() ,函數(shù)
,函數(shù)![]() 是增函數(shù);
是增函數(shù);
在區(qū)間![]() 上,
上, ![]() ,函數(shù)
,函數(shù)![]() 是減函數(shù);
是減函數(shù);
故在區(qū)間![]() 上,
上, ![]() 的極大值為
的極大值為![]() ,
,
由于![]() 無零點,須使
無零點,須使![]() ,解得
,解得![]() ,
,
故所求實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(3)要證![]() ,兩邊同時取自然對數(shù)得
,兩邊同時取自然對數(shù)得![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命題等價于證明![]() .
.
因為![]() ,故只需證
,故只需證![]() ,即
,即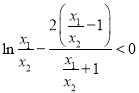 .
.
令![]() ,則
,則![]() ,設(shè)
,設(shè)![]() (
(![]() ),只需證
),只需證![]() .
.
而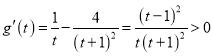 ,故
,故![]() 在
在![]() 單調(diào)遞增,所以
單調(diào)遞增,所以![]() .
.
綜上得![]() .
.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:9x2+y2=m2(m>0),直線l不過原點O且不平行于坐標軸,l與C有兩個交點A,B,線段AB的中點為M.
(1)證明:直線OM的斜率與l的斜率的乘積為定值;
(2)若l過點( ![]() ,m),延長線段OM與C交于點P,四邊形OAPB能否為平行四邊形?若能,求此時l的斜率;若不能,說明理由.
,m),延長線段OM與C交于點P,四邊形OAPB能否為平行四邊形?若能,求此時l的斜率;若不能,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量 ![]() =(﹣2,4),
=(﹣2,4), ![]() =(﹣1,﹣2).
=(﹣1,﹣2).
(1)求 ![]() ,
, ![]() 的夾角的余弦值;
的夾角的余弦值;
(2)若向量 ![]() ﹣λ
﹣λ ![]() 與2
與2 ![]() +
+ ![]() 垂直,求λ的值.
垂直,求λ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]()
(Ⅰ)當![]() (
(![]() 為自然對數(shù)的底數(shù))時,求
為自然對數(shù)的底數(shù))時,求![]() 的極小值;
的極小值;
(Ⅱ)若函數(shù)![]() 存在唯一零點,求
存在唯一零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等差數(shù)列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)設(shè)數(shù)列{an+bn}是首項為1,公比為c的等比數(shù)列,求{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題中錯誤的個數(shù)為:( )
①y= ![]() 的圖象關(guān)于(0,0)對稱;
的圖象關(guān)于(0,0)對稱;
②y=x3+x+1的圖象關(guān)于(0,1)對稱;
③y= ![]() 的圖象關(guān)于直線x=0對稱;
的圖象關(guān)于直線x=0對稱;
④y=sinx+cosx的圖象關(guān)于直線x= ![]() 對稱.
對稱.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)是定義在R上的偶函數(shù),對任意x∈R,都有f(x)=f(x+4),且當x∈[﹣2,0]時,f(x)=( ![]() )x﹣1,若在區(qū)間(﹣2,6]內(nèi)關(guān)于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三個不同的實數(shù)根,則a的取值范圍是( )
)x﹣1,若在區(qū)間(﹣2,6]內(nèi)關(guān)于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三個不同的實數(shù)根,則a的取值范圍是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某家庭進行理財投資,根據(jù)長期收益率市場預(yù)測,投資債券類穩(wěn)健型產(chǎn)品的收益與投資額成正比,投資股票類風(fēng)險型產(chǎn)品的收益與投資額的算術(shù)平方根成正比,已知兩類產(chǎn)品各投資1萬元時的收益分別為0.125萬元和0.5萬元,如圖:
(Ⅰ)分別寫出兩類產(chǎn)品的收益y(萬元)與投資額x(萬元)的函數(shù)關(guān)系;
(Ⅱ)該家庭有20萬元資金,全部用于理財投資,問:怎么分配資金能使投資獲得最大收益,最大收益是多少萬元?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com