
【題目】已知函數![]() .
.
(1)當b=4時,求![]() 的極值;
的極值;
(2)若![]() 在區間
在區間![]() 上單調遞增,求b的取值范圍.
上單調遞增,求b的取值范圍.
【答案】(1)極小值f(-2)=0,極大值f(0)=4;(2)![]()
【解析】
(1)求導,判斷函數的單調性,進而求出函數的極值;
(2)![]() 在區間
在區間![]() 上單調遞增,說明導函數在
上單調遞增,說明導函數在![]() 上大于或者等于零,求出
上大于或者等于零,求出![]() 的取值范圍.
的取值范圍.
(1)當b=4時,![]() ,
,
由f′(x)=0,得x=-2或x=0.
所以當x∈(-∞,-2)時,f′(x)<0,f(x)單調遞減;
當x∈(-2,0)時,f′(x)>0,f(x)單調遞增;
當x∈![]() 時,f′(x)<0,f(x)單調遞減,
時,f′(x)<0,f(x)單調遞減,
故f(x)在x=-2處取得極小值f(-2)=0,在x=0處取得極大值f(0)=4.
(2)f′(x)=![]() , 易知當x∈
, 易知當x∈![]() 時,
時,![]() <0,
<0,
依題意當x∈![]() 時,有5x+(3b-2)≤0,從而
時,有5x+(3b-2)≤0,從而![]() +(3b-2)≤0,得b≤
+(3b-2)≤0,得b≤![]() .
.
所以b的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示,正方體ABCD-A1B1C1D1中,M、N分別是A1B1、B1C1的中點,問:

(1)AM和CN是否是異面直線?說明理由;
(2)D1B和CC1是否是異面直線?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱臺![]() 中,上底面邊長為4,下底面邊長為8,高為5,點
中,上底面邊長為4,下底面邊長為8,高為5,點![]() 分別在
分別在![]() 上,且
上,且![]() .過點
.過點![]() 的平面
的平面![]() 與此四棱臺的下底面會相交,則平面
與此四棱臺的下底面會相交,則平面![]() 與四棱臺的面的交線所圍成圖形的面積的最大值為
與四棱臺的面的交線所圍成圖形的面積的最大值為

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由一組樣本數據 ![]() ,
,![]() ,
,![]() ,
,![]() 得到的回歸直線方程為
得到的回歸直線方程為![]() ,那么下面說法正確的序號________.
,那么下面說法正確的序號________.
(1) 直線![]() 必經過點
必經過點 ![]()
(2)直線![]() 至少經過點
至少經過點 ![]() ,
,![]() ,
,![]() ,
,![]() 中的一個
中的一個
(3)直線![]() 的斜率為
的斜率為 .
.
(4)回歸直線方程![]() 最能代表樣本數據中
最能代表樣本數據中![]() ,
,![]() 之間的線性關系,b大于0時
之間的線性關系,b大于0時![]() 與
與![]() 正相關,b小于0時
正相關,b小于0時![]() 與
與![]() 負相關.
負相關.
注:相關數據: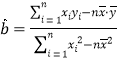 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某森林出現火災,火勢正以每分鐘![]() 的速度順風蔓延,消防站接到警報立即派消防隊員前去,在火災發生后
的速度順風蔓延,消防站接到警報立即派消防隊員前去,在火災發生后![]() 分鐘到達救火現場,已知消防隊員在現場平均每人每分鐘滅火
分鐘到達救火現場,已知消防隊員在現場平均每人每分鐘滅火![]() ,所消耗的滅火材料、勞務津貼等費用為每人每分鐘125元,另附加每次救火所損耗的車輛、器械和裝備等費用平均每人100元,而燒毀一平方米森林損失費為60元.
,所消耗的滅火材料、勞務津貼等費用為每人每分鐘125元,另附加每次救火所損耗的車輛、器械和裝備等費用平均每人100元,而燒毀一平方米森林損失費為60元.
(1)設派![]() 名消防隊員前去救火,用
名消防隊員前去救火,用![]() 分鐘將火撲滅,試建立
分鐘將火撲滅,試建立![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)問應該派多少名消防隊員前去救火,才能使總損失最少?
(總損失=滅火材料、勞務津貼等費用+車輛、器械和裝備費用+森林損失費)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某中學為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識的競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐、規定:每場知識競賽前三名的得分都分別為![]() (
(![]() ,且
,且![]() );選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為26分,乙和丙最后得分都為11分,且乙在其中一場比賽中獲得第一名,則下列推理正確的是( )
);選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為26分,乙和丙最后得分都為11分,且乙在其中一場比賽中獲得第一名,則下列推理正確的是( )
A. 每場比賽第一名得分![]() 為4 B. 甲可能有一場比賽獲得第二名
為4 B. 甲可能有一場比賽獲得第二名
C. 乙有四場比賽獲得第三名 D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個命題:①“若![]() ,則
,則![]() ,
,![]() 互為倒數”的逆命題;②“面積相等的三角形全等”的否命題;③“若
互為倒數”的逆命題;②“面積相等的三角形全等”的否命題;③“若![]() ,則
,則![]() 有實數解”的逆否命題;④“若
有實數解”的逆否命題;④“若![]() ,則
,則![]() ”的逆否命題.其中真命題為________(填寫所有真命題的序號).
”的逆否命題.其中真命題為________(填寫所有真命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,離心率
,離心率![]() .
.

(I)求橢圓C的標準方程;
(II)已知直線![]() 交橢圓C于A,B兩點.
交橢圓C于A,B兩點.
①若直線![]() 經過橢圓C的左焦點F,交y軸于點P,且滿足
經過橢圓C的左焦點F,交y軸于點P,且滿足![]() .求證:
.求證:![]() 為定值;
為定值;
②若![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com