
【題目】已知橢圓![]() 的左右焦點(diǎn)分別為
的左右焦點(diǎn)分別為![]() ,經(jīng)過(guò)點(diǎn)
,經(jīng)過(guò)點(diǎn)![]() 的直線(xiàn)與橢圓相交于
的直線(xiàn)與橢圓相交于![]() 兩點(diǎn),已知
兩點(diǎn),已知![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() 。
。
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,求直線(xiàn)
,求直線(xiàn)![]() 的方程。
的方程。
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:
(1)由![]() 可得
可得![]() ,由
,由![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() 可得
可得![]() ,求得
,求得![]() 可得橢圓的方程。(2)由題意設(shè)直線(xiàn)方程為
可得橢圓的方程。(2)由題意設(shè)直線(xiàn)方程為![]() ,代入橢圓方程消去x后得到方程
,代入橢圓方程消去x后得到方程![]() ,由根與系數(shù)的關(guān)系可得
,由根與系數(shù)的關(guān)系可得![]() ,又由
,又由![]() 得
得![]() ,從而可得
,從而可得![]() 。求得點(diǎn)D的坐標(biāo)后可得所求的直線(xiàn)方程。
。求得點(diǎn)D的坐標(biāo)后可得所求的直線(xiàn)方程。
試題解析:
(1)由題意得![]() ,所以
,所以![]() 。
。
又因?yàn)?/span>![]() ,所以
,所以![]() 。
。
所以![]() 。
。
故橢圓![]() 的方程為
的方程為![]() 。
。
(2)設(shè)![]() ,由
,由![]() ,可得
,可得![]() 。
。
又直線(xiàn)![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,可設(shè)直線(xiàn)
,可設(shè)直線(xiàn)![]() 的方程為
的方程為![]() ,
,
由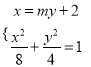 消去x整理得
消去x整理得
![]() ,
,
![]() 。
。
且![]() ,①
,①
又![]() ,②
,②
由①②消去![]() 得
得![]() ,
,
解得![]() 。
。
當(dāng)![]() 時(shí),可得
時(shí),可得![]() ,故
,故![]() ,此時(shí)點(diǎn)D的坐標(biāo)為
,此時(shí)點(diǎn)D的坐標(biāo)為![]() ,
,
故直線(xiàn)AD的方程為![]() 。
。
當(dāng)![]() 時(shí),可得
時(shí),可得![]() ,故
,故![]() ,此時(shí)點(diǎn)D的坐標(biāo)為
,此時(shí)點(diǎn)D的坐標(biāo)為![]() ,
,
故直線(xiàn)AD的方程為![]() 。
。
綜上可得直線(xiàn)![]() 的方程為
的方程為![]() 。
。


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知復(fù)數(shù)z=![]() ,(m∈R,i是虛數(shù)單位).
,(m∈R,i是虛數(shù)單位).
(1)若z是純虛數(shù),求m的值;
(2)設(shè)![]() 是z的共軛復(fù)數(shù),復(fù)數(shù)
是z的共軛復(fù)數(shù),復(fù)數(shù)![]() +2z在復(fù)平面上對(duì)應(yīng)的點(diǎn)在第一象限,求m的取值范圍.
+2z在復(fù)平面上對(duì)應(yīng)的點(diǎn)在第一象限,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的中心在原點(diǎn),短軸長(zhǎng)為
的中心在原點(diǎn),短軸長(zhǎng)為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓上.
在橢圓上.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若斜率為![]() 的直線(xiàn)
的直線(xiàn)![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),
兩點(diǎn), ![]() 為弦
為弦![]() 中點(diǎn),求點(diǎn)
中點(diǎn),求點(diǎn)![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】微信支付誕生于微信紅包,早期知識(shí)作為社交的一部分“發(fā)紅包”而誕生的,在發(fā)紅包之余才發(fā)現(xiàn),原來(lái)微信支付不僅可以用來(lái)發(fā)紅包,還可以用來(lái)支付,現(xiàn)在微信支付被越來(lái)越多的人們所接受,現(xiàn)從某市市民中隨機(jī)抽取300為對(duì)是否使用微信支付進(jìn)行調(diào)查,得到下列![]() 的列聯(lián)表:
的列聯(lián)表:
年輕人 | 非年輕人 | 總計(jì) | |
經(jīng)常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合計(jì) | 90 | 300 |
根據(jù)表中數(shù)據(jù),我們得到的統(tǒng)計(jì)學(xué)的結(jié)論是:由__________的把握認(rèn)為“使用微信支付與年齡有關(guān)”。
|
|
|
|
|
|
|
|
|
|
|
|
其中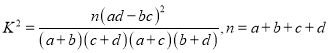
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(12分)已知函數(shù)f(x)=![]()
(1)判斷函數(shù)在區(qū)間[1,+∞)上的單調(diào)性,并用定義證明你的結(jié)論.
(2)求該函數(shù)在區(qū)間[1,4]上的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)集合![]() ,
,![]() ,
,
(1)若![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(2)若![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某家庭進(jìn)行理財(cái)投資,根據(jù)長(zhǎng)期收益率市場(chǎng)預(yù)測(cè),投資![]() 類(lèi)產(chǎn)品的收益與投資額成正比,投資
類(lèi)產(chǎn)品的收益與投資額成正比,投資![]() 類(lèi)產(chǎn)品的收益與投資額的算術(shù)平方根成正比.已知投資1萬(wàn)元時(shí)
類(lèi)產(chǎn)品的收益與投資額的算術(shù)平方根成正比.已知投資1萬(wàn)元時(shí)![]() 兩類(lèi)產(chǎn)品的收益分別為0.125萬(wàn)元和0.5萬(wàn)元.
兩類(lèi)產(chǎn)品的收益分別為0.125萬(wàn)元和0.5萬(wàn)元.
(1)分別寫(xiě)出![]() 兩類(lèi)產(chǎn)品的收益與投資額的函數(shù)關(guān)系;
兩類(lèi)產(chǎn)品的收益與投資額的函數(shù)關(guān)系;
(2)該家庭有20萬(wàn)元資金,全部用于理財(cái)投資,問(wèn):怎么分配資金能使投資獲得最大收益,其最大收益是多少萬(wàn)元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在定義域內(nèi)為增函數(shù),求實(shí)數(shù)
在定義域內(nèi)為增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的極小值;
的極小值;
(3)設(shè)![]() ,
, ![]() .若函數(shù)
.若函數(shù)![]() 存在兩個(gè)零點(diǎn)
存在兩個(gè)零點(diǎn)![]() ,且滿(mǎn)足
,且滿(mǎn)足![]() ,問(wèn):函數(shù)
,問(wèn):函數(shù)![]() 在
在![]() 處的切線(xiàn)能否平行于
處的切線(xiàn)能否平行于![]() 軸?若能,求出該切線(xiàn)方程,若不能,請(qǐng)說(shuō)明理由.
軸?若能,求出該切線(xiàn)方程,若不能,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一次趣味校園運(yùn)動(dòng)會(huì)的頒獎(jiǎng)儀式上,高一、高二、高三代表隊(duì)人數(shù)分別為120人、120人、n人.為了活躍氣氛,大會(huì)組委會(huì)在頒獎(jiǎng)過(guò)程中穿插抽獎(jiǎng)活動(dòng),并用分層抽樣的方法從三個(gè)代表隊(duì)中共抽取20人在前排就座,其中高二代表隊(duì)有6人.

(1)求n的值;
(2)把在前排就座的高二代表隊(duì)6人分別記為a,b,c,d,e,f,現(xiàn)隨機(jī)從中抽取2人上臺(tái)抽獎(jiǎng).求a和b至少有一人上臺(tái)抽獎(jiǎng)的概率;
(3)抽獎(jiǎng)活動(dòng)的規(guī)則是:代表通過(guò)操作按鍵使電腦自動(dòng)產(chǎn)生兩個(gè)[0,1]之間的均勻隨機(jī)數(shù)x,y,并按如圖所示的程序框圖執(zhí)行.若電腦顯示“中獎(jiǎng)”,則該代表中獎(jiǎng);若電腦顯示“謝謝”,則不中獎(jiǎng),求該代表中獎(jiǎng)的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com