
【題目】學校游園活動有這樣一個游戲:甲箱子里裝有3個白球,2個黑球,乙箱子里裝有1個白球,2個黑球,這些球除了顏色外完全相同,每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎(每次游戲結束后將球放回原箱).
(1)求在1次游戲中:
①摸出3個白球的概率.
②獲獎的概率.
(2)求在3次游戲中獲獎次數X的分布列.(用數字作答)
【答案】
(1)解:①設“在1次游戲中摸到i個白球”為事件Ai(i=0,1,2,3),
則P(A3)= ![]() =
= ![]() ;
;
②設“在一次游戲中獲獎”為事件B,則B=A2∪A3,
又P(A2)= ![]()
![]() +
+ ![]()
![]() =
= ![]() ,且A2、A3互斥,
,且A2、A3互斥,
所以P(B)=P(A2)+P(A3)= ![]() +
+ ![]() =
= ![]()
(2)解:由題意可知X的所有可能取值為0,1,2,3;
P(X=0)= ![]() (1﹣
(1﹣ ![]() )3=
)3= ![]() ,
,
P(X=1)=C31 ![]()
![]() =
= ![]() ,
,
P(X=2)= ![]()
![]() (1﹣
(1﹣ ![]() )=
)= ![]() ,
,
P(X=3)= ![]()
![]() =
= ![]() ;
;
所以X的分布列為
X | 0 | 1 | span>2 | 3 |
P |
|
|
|
|
【解析】(1)①求出基本事件總數,計算摸出3個白球事件數,利用古典概型公式,代入數據得到結果;②獲獎包含摸出2個白球和摸出3個白球,且它們互斥,根據①求出摸出2個白球的概率,再相加即可求得結果;(2)確定在3次游戲中獲獎次數X的取值是0、1、2、3,求出相應的概率,即可寫出分布列.
【考點精析】解答此題的關鍵在于理解離散型隨機變量及其分布列的相關知識,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】若f(x)=x2﹣x+b,且f(log2a)=b,log2[f(a)]=2(a≠1).
(1)求f(log2x)的最小值及對應的x值;
(2)x取何值時,f(log2x)>f(1)且log2[f(x)]<f(1)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,四邊形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H為BC的中點.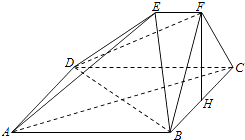
(1)求證:FH∥平面EDB;
(2)求證:AC⊥平面EDB;
(3)解:求二面角B﹣DE﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() 為集合
為集合![]() 的
的![]() 個非空子集,這
個非空子集,這![]() 個集合滿足:①從中任取
個集合滿足:①從中任取![]() 個集合都有
個集合都有![]()
![]()
![]() 成立;②從中任取
成立;②從中任取![]() 個集合都有
個集合都有![]()
![]() 成立.
成立.
(Ⅰ)若![]() ,
, ![]() ,
, ![]() ,寫出滿足題意的一組集合
,寫出滿足題意的一組集合![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,寫出滿足題意的一組集合
,寫出滿足題意的一組集合![]() 以及集合
以及集合![]() ;
;
(Ⅲ) 若![]() ,
, ![]() ,求集合
,求集合![]() 中的元素個數的最小值.
中的元素個數的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)若f(x)在( ![]() ,+∞)上是單調減函數,求實數a的取值范圍.
,+∞)上是單調減函數,求實數a的取值范圍.
(2)當0<a<2時,f(x)在[1,4]上的最小值為﹣ ![]() ,求f(x)在該區間的最大值.
,求f(x)在該區間的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,點
為菱形,點![]() 是棱
是棱![]() 上不同于
上不同于![]() ,
, ![]() 的點,平面
的點,平面![]() 與棱
與棱![]() 交于點
交于點![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求證: ![]() 平面
平面![]() ;
;
(Ⅲ)若二面角![]() 為
為![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知偶函數f(x)的定義域為R,且在(﹣∞,0)上是增函數,則f(﹣ ![]() )與f(a2﹣a+1)的大小關系為( )
)與f(a2﹣a+1)的大小關系為( )
A.f(﹣ ![]() )<f(a2﹣a+1)
)<f(a2﹣a+1)
B.f(﹣ ![]() )>f(a2﹣a+1)??
)>f(a2﹣a+1)??
C.f(﹣ ![]() )≤f(a2﹣a+1)
)≤f(a2﹣a+1)
D.f(﹣ ![]() )≥f(a2﹣a+1)
)≥f(a2﹣a+1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com