Question

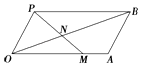
【題目】如圖所示，四邊形OABP是平行四邊形，過點P的直線與射線OA，OB分別相交于點M，N，若 ， ．

（1）把y用x表示出來（即求y=f（x）的解析式）；
（2）設數列{an}的首項a1=1，前n項和Sn滿足Sn=f（Sn﹣1）（n≥2且n∈N*），求數列{an}的通項公式．

Answer 1

【答案】
（1）解：∵ ， ，

∴ =x， ，∴ ，

∵△OMN∽△BPN，

∴ ，

∴ ，

∴y=f（x）=

（2）解：Sn=f（Sn﹣1）= ，

∴ = ，∴ ﹣ =1，

∵S1=a1=1，∴數列{ }是首項為1，公差為1的等差數列，

∴ =n，即Sn= ，

當n≥2時，an=Sn﹣Sn﹣1= ﹣ = ．

∴an=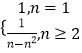

【解析】（1）利用 得出方程得出f（x）；（2）對Sn=f（Sn﹣1）= 取倒數，即可得出{ }為等差數列，從而求出Sn ， 再利用an= ．
【考點精析】本題主要考查了平面向量的基本定理及其意義的相關知識點，需要掌握如果、是同一平面內的兩個不共線向量，那么對于這一平面內的任意向量，有且只有一對實數、，使才能正確解答此題．