
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的零點;
的零點;
(2)若![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的最小值
上的最小值![]() .
.
【答案】(1) ![]() ,
,![]() ,
,![]() . (2)
. (2) 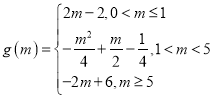
【解析】
(1)函數![]() 的零點等價于方程
的零點等價于方程![]() 的解;
的解;
(2)對![]() 分四種情況進行討論,即
分四種情況進行討論,即![]() ,
,![]() ,
,![]() ,
,![]() 分別每種情況各自的最小值,最后再討論
分別每種情況各自的最小值,最后再討論![]() 對最小值進行整合.
對最小值進行整合.
(1)當![]() 時,函數
時,函數![]() 的零點等價于方程
的零點等價于方程![]() 的解,
的解,
所以![]() 或
或![]() ,
,
所以或![]() 或
或![]() 或
或![]() ,
,
即函數![]() 的零點為
的零點為![]() ,
,![]() ,
,![]() .
.
(2)因為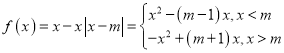 ,
,
![]() 當
當![]() 時,
時,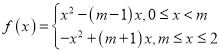 ,
,
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單增,
上單增,
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單增,在
上單增,在![]() 上單減,
上單減,
所以,函數![]() 在
在![]() 上的最小值
上的最小值![]()
![]() .
.
![]() 當
當![]() 時,
時,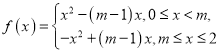 ,
,
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,
上單增,
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單減,
上單減,
所以,函數![]() 在
在![]() 上的最小值
上的最小值![]()
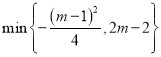 .
.
因為![]()
![]()
所以當![]() 時,
時,![]() ,
,
即此時函數![]() 在
在![]() 上的最小值
上的最小值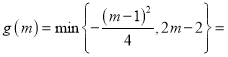
![]() ,
,
![]() 當
當![]() 時,
時,![]() ,
,![]()
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單減,在
上單減,在![]() 上單增,
上單增,
所以,函數![]() 在
在![]() 上的最小值
上的最小值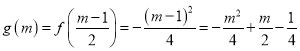 ,
,
![]() 當
當![]() 時,
時,![]() ,
,![]()
因為![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上單減,
上單減,
所以,函數![]() 在
在![]() 上的最小值
上的最小值![]() .
.
綜上,函數![]() 在
在![]() 上的最小值.
上的最小值.
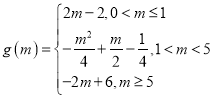 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在一個風雨交加的夜里,某水庫閘房(設為A)到某指揮部(設為B)的電話線路有一處發生了故障.這是一條![]() 長的線路,想要盡快地查出故障所在.如果沿著線路一小段小段地查找,困難很多,每查一小段需要很長時間.
長的線路,想要盡快地查出故障所在.如果沿著線路一小段小段地查找,困難很多,每查一小段需要很長時間.
(1)維修線路的工人師傅隨身帶著話機,他應怎樣工作,才能每查一次,就把待查的線路長度縮減一半?
(2)要把故障可能發生的范圍縮小到![]() ,最多要查多少次?
,最多要查多少次?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,已知
,已知![]() ,其中
,其中![]() 為原點,
為原點,![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線的
,求直線的![]() 斜率的取值范圍.
斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,
,![]() ,
,![]() 分別為左、右焦點,過
分別為左、右焦點,過![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為8.
的周長為8.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線交橢圓
的直線交橢圓![]() 于不同兩點
于不同兩點![]() ,
,![]() .
.![]() 為橢圓上一點,且滿足
為橢圓上一點,且滿足![]() (
(![]() 為坐標原點),當
為坐標原點),當![]() 時,求實數
時,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河北保定市上學期期末調研】已知點![]() 到點
到點![]() 的距離比到
的距離比到![]() 軸的距離大1.
軸的距離大1.
(I)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(II)設直線![]() :
: ![]() ,交軌跡
,交軌跡![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 為坐標原點,試在軌跡
為坐標原點,試在軌跡![]() 的
的![]() 部分上求一點
部分上求一點![]() ,使得
,使得![]() 的面積最大,并求其最大值.
的面積最大,并求其最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com