Question

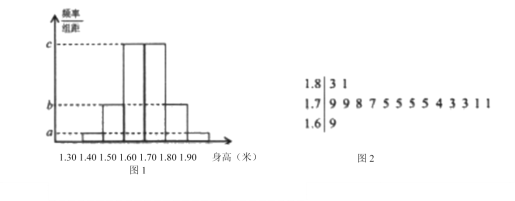
【題目】某市教育部門為了解全市高三學生的身高發育情況，從本市全體高三學生中隨機抽取了100人的身高數據進行統計分析．經數據處理后，得到了如下圖1所示的頻事分布直方圖，并發現這100名學生中，身高不低于1.69米的學生只有16名，其身高莖葉圖如下圖2所示，用樣本的身高頻率估計該市高一學生的身高概率．

（1）求該市高三學生身高高于1.70米的概率，并求圖1中、、的值．

（2）若從該市高三學生中隨機選取3名學生，記為身高在的學生人數，求的分布列和數學期望；

（3）若變量滿足且，則稱變量滿足近似于正態分布的概率分布．如果該市高三學生的身高滿足近似于正態分布的概率分布，則認為該市高三學生的身高發育總體是正常的．試判斷該市高三學生的身高發育總體是否正常，并說明理由．

Answer 1

【答案】（1）概率為0.15．，，．（2）見解析（3）正常

【解析】分析：（1）先利用概率公式求這批學生的身高高于1.70的概率，再求、、，從而得到a,b,c的值.(2)由于隨機變量服從二項分布，根據二項分布求的分布列和數學期望.(3)先求、，再根據已知判斷該市高三學生的身高發育總體是否正常.

詳解：（1）由圖2可知，100名樣本學生中身高高于1.70米共有15名，以樣本的頻率估計總體的概率，可得這批學生的身高高于1.70的概率為0.15．

記為學生的身高，結合圖1可得：

，

，

，

又由于組距為0.1，所以，，．

（2）以樣本的頻率估計總體的概率，

可知從這批學生中隨機選取1名，身高在的概率為

，

因為從這批學生中隨機選取3名，相當于三次重復獨立試驗，

所以隨機變量服從二項分布，

分布列為：，

	0	1	2	3
	0.027	0.189	0.441	0.343

（或）

（3）由，取，，

由（2）可知，，

又結合（1），可得：，

，

所以這批學生的身高滿足近似于正態分布的概率分布，應該認為該市高一學生的身高發育總體是正常的．