
【題目】設函數![]() .
.
(1)當![]() 時,設
時,設![]() ,求證:對任意的
,求證:對任意的![]() ,
,![]() ;
;
(2)當![]() 時,若對任意
時,若對任意![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)當![]() 時,原不等式等價于
時,原不等式等價于![]() .令
.令![]() ,求導后可知函數
,求導后可知函數![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,得證;(2)當
,得證;(2)當![]() 時,原不等式等價于
時,原不等式等價于![]() ,令
,令![]() ,
,![]() ,對
,對![]() 求導后對
求導后對![]() 分成
分成![]() ,
,![]() 兩類討論,可求得實數
兩類討論,可求得實數![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析:
(1)當![]() 時,
時,![]() ,
,
所以![]() 等價于
等價于![]() .
.
令![]() ,則
,則![]() ,可知函數
,可知函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,即
,即![]() ,亦即
,亦即![]()
(2)當![]() 時,
時,![]() ,
,![]() .
.
所以不等式![]() 等價于
等價于![]() .
.
方法一:令![]() ,
,![]() ,
,
則![]() .
.
當![]() 時,
時,![]() ,則函數
,則函數![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
所以根據題意,知有![]() ,∴
,∴![]()
當![]() 時,由
時,由![]() ,知函數
,知函數![]() 在
在![]() 上單調減;
上單調減;
由![]() ,知函數
,知函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() .
.
由條件知,![]() ,即
,即![]() .
.
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
所以![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,所以
,所以![]() 與條件矛盾.
與條件矛盾.
綜上可知,實數![]() 的取值范圍為
的取值范圍為![]() .
.
方法二:令![]() ,
,![]() ,
,
則![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
所以![]() .
.
又![]() ,
,
顯然當![]() 時,
時,![]() ,則函數
,則函數![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,所以
,所以![]() .
.
綜上可知![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某班一次數學考試成績頻率分布直方圖如圖所示,數據分組依次為![]() ,已知成績大于等于
,已知成績大于等于![]() 分的人數為
分的人數為![]() 人,現采用分層抽樣的方式抽取一個容量為
人,現采用分層抽樣的方式抽取一個容量為![]() 的樣本.
的樣本.
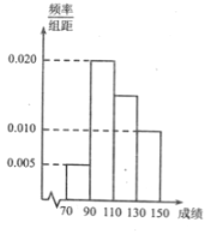
(1)求每個分組所抽取的學生人數;
(2)從數學成績在![]() 的樣本中任取
的樣本中任取![]() 人,求恰有
人,求恰有![]() 人成績在
人成績在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合I={1,2,3,4,5},選擇I的兩個非空子集A和B,要使B中最小的數大于A中最大的數,則不同的選擇方法共有
A.50種 B.49種 C.48種 D.47種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程,在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為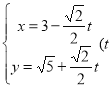 為參數),在極坐標系(與直角坐標系
為參數),在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極軸,以
為極軸,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的圓心到直線
的圓心到直線![]() 的距離;
的距離;
(2)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司今年年初用25萬元引進一種新的設備,投入設備后每年收益為21萬元。該公司第n年需要付出設備的維修和工人工資等費用![]() 的信息如下圖。
的信息如下圖。
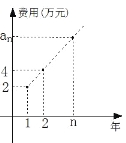
(Ⅰ)求![]() ;
;
(Ⅱ)引進這種設備后,第幾年后該公司開始獲利;
(Ⅲ)這種設備使用多少年,該公司的年平均獲利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程:
的方程:![]()
(1)求m的取值范圍;
(2)若圓C與直線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圓與直線x+2y-4=0相交于M、N兩點,且OM⊥ON(O為坐標原點),求m的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com