
已知函數(shù)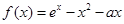 ,如果函數(shù)
,如果函數(shù) 恰有兩個(gè)不同的極值點(diǎn)
恰有兩個(gè)不同的極值點(diǎn)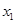 ,
,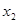 ,且
,且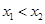 .
.
(Ⅰ)證明: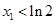 ;
;
(Ⅱ)求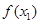 的最小值,并指出此時(shí)
的最小值,并指出此時(shí)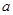 的值.
的值.
(Ⅰ)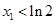 ;(Ⅱ)
;(Ⅱ)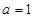 .
.
解析試題分析:(Ⅰ)因?yàn)?函數(shù) 恰有兩個(gè)不同的極值點(diǎn)
恰有兩個(gè)不同的極值點(diǎn)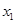 ,
,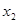 ,即
,即 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)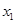 ,
,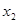 ,則
,則
方程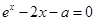 有兩個(gè)不同的零點(diǎn)
有兩個(gè)不同的零點(diǎn)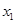 ,
,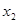 ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)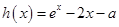 ,求導(dǎo)
,求導(dǎo)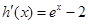 ,
,
當(dāng)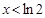 時(shí),
時(shí), ,
,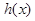 是減函數(shù);當(dāng)
是減函數(shù);當(dāng)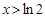 時(shí),
時(shí),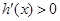 ,
,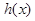 是增函數(shù),所以
是增函數(shù),所以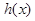 在
在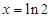 時(shí)取得最小值.∴
時(shí)取得最小值.∴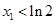 .(Ⅱ)由(Ⅰ)知
.(Ⅱ)由(Ⅰ)知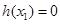 ,即
,即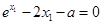 ,所以
,所以  ,
,
于是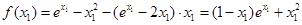 ,所以
,所以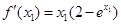 ,
,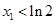 ,所以
,所以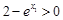 .所以 當(dāng)
.所以 當(dāng)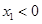 時(shí),
時(shí), ,
,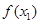 是減函數(shù);當(dāng)
是減函數(shù);當(dāng)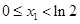 時(shí),
時(shí),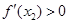 ,
,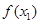 是增函數(shù),所以
是增函數(shù),所以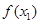 在
在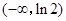 上的最小值為
上的最小值為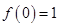 ,此時(shí)
,此時(shí)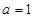 .
.
試題解析:(Ⅰ)∵ 函數(shù) 恰有兩個(gè)不同的極值點(diǎn)
恰有兩個(gè)不同的極值點(diǎn)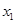 ,
,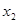 ,即
,即 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)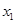 ,
,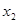
∴ 方程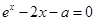 有兩個(gè)不同的零點(diǎn)
有兩個(gè)不同的零點(diǎn)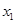 ,
,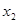
令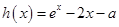 .
.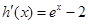 ,
,
當(dāng)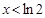 時(shí),
時(shí), ,
,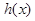 是減函數(shù);
是減函數(shù);
當(dāng)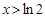 時(shí),
時(shí),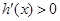 ,
,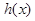 是增函數(shù),
是增函數(shù),
∴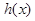 在
在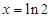 時(shí)取得最小值.
時(shí)取得最小值.
∴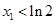 .
.
(Ⅱ)∵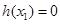 ,即
,即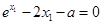 ,
,
∴
于是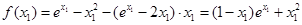 ,
,
∴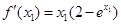
∵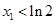 ,
,
∴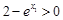 .
.
∴ 當(dāng)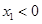 時(shí),
時(shí), ,
,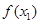 是減函數(shù);
是減函數(shù);
當(dāng)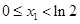 時(shí),
時(shí),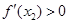 ,
,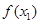 是增函數(shù)
是增函數(shù)
∴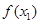 在
在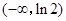 上的最小值為
上的最小值為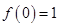 ,此時(shí)
,此時(shí)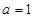 .
.
考點(diǎn):1.函數(shù)中證明問(wèn)題;3.函數(shù)與不等式的綜合應(yīng)用.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
湖北省第十四屆運(yùn)動(dòng)會(huì)紀(jì)念章委托某專(zhuān)營(yíng)店銷(xiāo)售,每枚進(jìn)價(jià)5元,同時(shí)每銷(xiāo)售一枚這種紀(jì)念章需向荊州籌委會(huì)交特許經(jīng)營(yíng)管理費(fèi)2元,預(yù)計(jì)這種紀(jì)念章以每枚20元的價(jià)格銷(xiāo)售時(shí)該店一年可銷(xiāo)售2000枚,經(jīng)過(guò)市場(chǎng)調(diào)研發(fā)現(xiàn)每枚紀(jì)念章的銷(xiāo)售價(jià)格在每枚20元的基礎(chǔ)上每減少一元?jiǎng)t增加銷(xiāo)售400枚,而每增加一元?jiǎng)t減少銷(xiāo)售100枚,現(xiàn)設(shè)每枚紀(jì)念章的銷(xiāo)售價(jià)格為 元,
元, 為整數(shù).
為整數(shù).
(1)寫(xiě)出該專(zhuān)營(yíng)店一年內(nèi)銷(xiāo)售這種紀(jì)念章所獲利潤(rùn)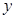 (元)與每枚紀(jì)念章的銷(xiāo)售價(jià)格
(元)與每枚紀(jì)念章的銷(xiāo)售價(jià)格 (元)的函數(shù)關(guān)系式(并寫(xiě)出這個(gè)函數(shù)的定義域);
(元)的函數(shù)關(guān)系式(并寫(xiě)出這個(gè)函數(shù)的定義域);
(2)當(dāng)每枚紀(jì)念章銷(xiāo)售價(jià)格 為多少元時(shí),該特許專(zhuān)營(yíng)店一年內(nèi)利潤(rùn)
為多少元時(shí),該特許專(zhuān)營(yíng)店一年內(nèi)利潤(rùn)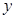 (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
用一塊鋼錠燒鑄一個(gè)厚度均勻,且表面積為2m2的正四棱錐形有蓋容器(如下圖)。設(shè)容器高為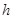 m,蓋子邊長(zhǎng)為
m,蓋子邊長(zhǎng)為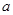 m,
m,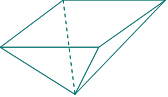
(1)求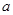 關(guān)于
關(guān)于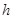 的解析式;
的解析式;
(2)設(shè)容器的容積為V m3,則當(dāng)h為何值時(shí),V最大? 并求出V的最大值(求解本題時(shí),不計(jì)容器厚度).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
集合A是由適合以下性質(zhì)的函數(shù) 構(gòu)成的:對(duì)于定義域內(nèi)任意兩個(gè)不相等的實(shí)數(shù)
構(gòu)成的:對(duì)于定義域內(nèi)任意兩個(gè)不相等的實(shí)數(shù)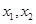 ,都有
,都有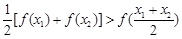 .
.
(1)試判斷 =
=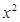 及
及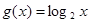 是否在集合A中,并說(shuō)明理由;
是否在集合A中,并說(shuō)明理由;
(2)設(shè) ÎA且定義域?yàn)?0,+¥),值域?yàn)?0,1),
ÎA且定義域?yàn)?0,+¥),值域?yàn)?0,1), ,試寫(xiě)出一個(gè)滿足以上條件的函數(shù)
,試寫(xiě)出一個(gè)滿足以上條件的函數(shù) 的解析式,并給予證明.
的解析式,并給予證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
對(duì)于函數(shù)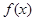 若存在
若存在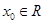 ,使得
,使得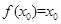 成立,則稱(chēng)
成立,則稱(chēng)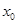 為
為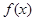 的不動(dòng)點(diǎn).
的不動(dòng)點(diǎn).
已知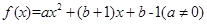
(1)當(dāng)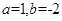 時(shí),求函數(shù)
時(shí),求函數(shù) 的不動(dòng)點(diǎn);
的不動(dòng)點(diǎn);
(2)若對(duì)任意實(shí)數(shù)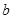 ,函數(shù)
,函數(shù)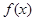 恒有兩個(gè)相異的不動(dòng)點(diǎn),求
恒有兩個(gè)相異的不動(dòng)點(diǎn),求 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若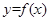 圖象上
圖象上 、
、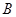 兩點(diǎn)的橫坐標(biāo)是函數(shù)
兩點(diǎn)的橫坐標(biāo)是函數(shù)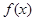 的不動(dòng)點(diǎn),且
的不動(dòng)點(diǎn),且 、
、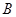 兩點(diǎn)關(guān)于直線
兩點(diǎn)關(guān)于直線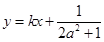 對(duì)稱(chēng),求
對(duì)稱(chēng),求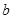 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某分公司經(jīng)銷(xiāo)某種品牌產(chǎn)品,每件產(chǎn)品的成本為30元,并且每件產(chǎn)品須向總公司繳納a元(a為常數(shù),2≤a≤5)的管理費(fèi),根據(jù)多年的統(tǒng)計(jì)經(jīng)驗(yàn),預(yù)計(jì)當(dāng)每件產(chǎn)品的售價(jià)為x元時(shí),產(chǎn)品一年的銷(xiāo)售量為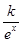 (e為自然對(duì)數(shù)的底數(shù))萬(wàn)件,已知每件產(chǎn)品的售價(jià)為40元時(shí),該產(chǎn)品一年的銷(xiāo)售量為500萬(wàn)件.經(jīng)物價(jià)部門(mén)核定每件產(chǎn)品的售價(jià)x最低不低于35元,最高不超過(guò)41元.
(e為自然對(duì)數(shù)的底數(shù))萬(wàn)件,已知每件產(chǎn)品的售價(jià)為40元時(shí),該產(chǎn)品一年的銷(xiāo)售量為500萬(wàn)件.經(jīng)物價(jià)部門(mén)核定每件產(chǎn)品的售價(jià)x最低不低于35元,最高不超過(guò)41元.
(Ⅰ)求分公司經(jīng)營(yíng)該產(chǎn)品一年的利潤(rùn)L(x)萬(wàn)元與每件產(chǎn)品的售價(jià)x元的函數(shù)關(guān)系式;
(Ⅱ)當(dāng)每件產(chǎn)品的售價(jià)為多少元時(shí),該產(chǎn)品一年的利潤(rùn)L(x)最大,并求出L(x)的最大值.
參考公式: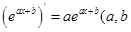 為常數(shù)
為常數(shù)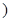 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知某公司生產(chǎn)品牌服裝的年固定成本為10萬(wàn)元,每生產(chǎn)千件,須另投入2.7萬(wàn)元,設(shè)該公司年內(nèi)共生產(chǎn)品牌服裝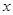 千件并全部銷(xiāo)售完,每千件的銷(xiāo)售收入為
千件并全部銷(xiāo)售完,每千件的銷(xiāo)售收入為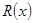 萬(wàn)元,且
萬(wàn)元,且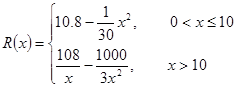 .
.
(1)寫(xiě)出年利潤(rùn)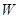 (萬(wàn)元)關(guān)于年產(chǎn)量
(萬(wàn)元)關(guān)于年產(chǎn)量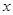 (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)當(dāng)年產(chǎn)量為多少千件時(shí),該公司在這一品牌服裝的生產(chǎn)中所獲年利潤(rùn)最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
統(tǒng)計(jì)表明:某種型號(hào)的汽車(chē)在勻速行駛中每小時(shí)的耗油量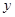 (升)關(guān)于行駛速度
(升)關(guān)于行駛速度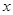 (千米/每小時(shí))的函數(shù)解析式可以表示為
(千米/每小時(shí))的函數(shù)解析式可以表示為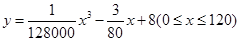 ,已知甲、乙兩地相距100千米.
,已知甲、乙兩地相距100千米.
(1)當(dāng)汽車(chē)以40千米/小時(shí)的速度行駛時(shí),從甲地到乙地要耗油多少升?
(2)當(dāng)汽車(chē)以多大速度行駛時(shí),從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com