
【題目】已知函數f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)當a=![]() 1時,求函數y=f(x)的單調區間;
1時,求函數y=f(x)的單調區間;
(2)求函數y=f(x)的極值點.
【答案】(1)遞增區間為(-∞,+∞);(2)見解析
【解析】
(1)先求解導數,利用導數取值的正負可得單調區間;
(2)先求解導數,結合導數零點情況判斷函數極值點的情況.
(1)當a=![]() 1時,
1時,![]() .∵
.∵![]() =x2
=x2![]() 2x+1=(x
2x+1=(x![]() 1)2≥0,
1)2≥0,
故函數在R內為增函數,單調遞增區間為(-∞,+∞).
(2)∵![]() =x2
=x2![]() (a2+a+2)x+a2(a+2)=(x
(a2+a+2)x+a2(a+2)=(x![]() a2)[x
a2)[x![]() (a+2)],
(a+2)],
①當a=![]() 1或a=2時,a2=a+2,∵
1或a=2時,a2=a+2,∵![]() ≥0恒成立,函數為增函數,無極值;
≥0恒成立,函數為增函數,無極值;
②當a<![]() 1或a>2時,a2>a+2,
1或a>2時,a2>a+2,
可得當x∈(![]() ∞,a+2)時,
∞,a+2)時,![]() >0,函數為增函數;
>0,函數為增函數;
當x∈(a+2,a2)時,![]() <0,函數為減函數;
<0,函數為減函數;
當x∈(a2,+∞)時,![]() >0,函數為增函數.
>0,函數為增函數.
當x=a+2時,函數有極大值f(a+2),當x=a2時,函數有極小值f(a2).
③當![]() 1<a<2時,a2<a+2.
1<a<2時,a2<a+2.
可得當x∈(-∞,a2)時,![]() >0,函數為增函數;
>0,函數為增函數;
當x∈(a2,a+2)時,![]() <0,函數為減函數;
<0,函數為減函數;
當x∈(a+2,+∞)時,![]() >0,函數為增函數.
>0,函數為增函數.
當x=a+2時,函數有極小值f(a+2);當x=a2時,函數有極大值f(a2).
綜上可得:當a=![]() 1或a=2時,函數無極值點;當a<
1或a=2時,函數無極值點;當a<![]() 1或a>2時,函數有極大值點a+2,函數有極小值點a2;當
1或a>2時,函數有極大值點a+2,函數有極小值點a2;當![]() 1<a<2時,函數有極大值點a2,函數有極小值點a+2.
1<a<2時,函數有極大值點a2,函數有極小值點a+2.


科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與x,y軸分別交于A,B兩點,0為坐標原點,且△OAB 的面積的最小值為
與x,y軸分別交于A,B兩點,0為坐標原點,且△OAB 的面積的最小值為![]()

(1)求橢圓![]() 的離心率;
的離心率;
(2) 設點C、D、F2分別為橢圓![]() 的上、下頂點以及右焦點,E 為線段OD 的中點,直線F2E 與橢圓
的上、下頂點以及右焦點,E 為線段OD 的中點,直線F2E 與橢圓![]() 相交于M、N 兩點,若
相交于M、N 兩點,若![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線Cn:x2﹣2nx+y2=0,(n=1,2,…).從點P(﹣1,0)向曲線Cn引斜率為kn(kn>0)的切線ln,切點為Pn(xn,yn).
(1)求數列{xn}與{yn}的通項公式;
(2)證明: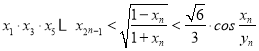 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱世杰是元代著名數學家,他所著《算學啟蒙》是一部在中國乃至世界最早的科學普及著作.《算學啟蒙》中提到一些堆垛問題,如“三角垛果子”,就是將一樣大小的果子堆垛成正三棱錐,每層皆堆成正三角形,從上向下數,每層果子數分別為1,3,6,10,…,現有一個“三角垛果子”,其最底層每邊果子數為10,則該層果子數為( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的長軸長為4,左、右頂點分別為
的長軸長為4,左、右頂點分別為![]() ,經過點
,經過點![]() 的動直線與橢圓
的動直線與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() (不與點
(不與點![]() 重合).
重合).
(1)求橢圓![]() 的方程及離心率;
的方程及離心率;
(2)求四邊形![]() 面積的最大值;
面積的最大值;
(3)若直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,判斷點
,判斷點![]() 是否位于一條定直線上?若是,寫出該直線的方程. (結論不要求證明)
是否位于一條定直線上?若是,寫出該直線的方程. (結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 與x軸交于A,B兩點,點Q的坐標為
與x軸交于A,B兩點,點Q的坐標為![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,說明理由;
,如果存在求出b值;如果不存在,說明理由;
(2)過A,B,Q三點的圓面積最小時,求圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為6,離心率為
的長軸長為6,離心率為![]() .
.
(1)求橢圓C的標準方程;
(2)設橢圓C的左、右焦點分別為![]() ,
,![]() ,左、右頂點分別為A,B,點M,N為橢圓C上位于x軸上方的兩點,且
,左、右頂點分別為A,B,點M,N為橢圓C上位于x軸上方的兩點,且![]() ,記直線AM,BN的斜率分別為
,記直線AM,BN的斜率分別為![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com