【題目】已知函數
．
（1）求函數
的最小正周期；
（2）若函數
對任意
，有
，求函數在[﹣
，
]上的值域．
【答案】（1）
（2）
【解析】試題分析：（1）逆用正弦的和角公式及降冪公式，可化得f(x)= 
sin2x+，由公式
可求得周期。（2）由題意可得g(x)
, 由
[﹣
，
]，求得整體角范圍2x+
∈
，則
≤sin（2x+
）≤1，可求得值域。
試題解析：（1）f（x）=
sin（2x+
）+sin2x
=
=
sin2x+cos2x+sin2x
=sin2x+
=sin2x+1﹣=sin2x+，
∴f（x）的最小正周期T=
；
（2）∵函數g（x）對任意x∈R，有g（x）=f（x+
），
∴g（x）=sin2（x+）+
=sin（2x+）+，
當x∈[﹣
，
]時，則2x+∈，
則≤sin（2x+）≤1，即×
≤g（x）
，解得
≤g（x）≤1．
綜上所述，函數g（x）在[﹣
，
]上的值域為：[
，1]．
科目：高中數學 來源： 題型：
【題目】如圖，六面體ABCDHEFG中，四邊形ABCD為菱形，AE，BF，CG，DH都垂直于平面ABCD.若DA＝DH＝DB＝4，AE＝CG＝3。
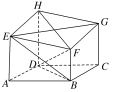
(1)求證：EG⊥DF；
(2)求BE與平面EFGH所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點P(2，2)，圓C：x2＋y2－8y＝0，過點P的動直線l與圓C交于A，B兩點，線段AB的中點為M，O為坐標原點．
(1)求M的軌跡方程；
(2)當|OP|＝|OM|時，求l的方程及△POM的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產一種電子儀器的固定成本為20 000元，每生產一臺儀器需要增加投入100元，已知總收益滿足函數：R(x)＝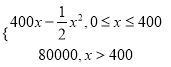
其中x是儀器的月產量．當月產量為何值時，公司所獲得利潤最大？最大利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】化為推出一款6寸大屏手機，現對500名該手機使用者（200名女性，300名男性）進行調查，對手機進行打分，打分的頻數分布表如下：
女性用戶：
分值區間 |
|
|
|
|
|
頻數 | 20 | 40 | 80 | 50 | 10 |
分值區間 |
|
|
|
|
|
頻數 | 45 | 75 | 90 | 60 | 30 |
男性用戶：
（1）如果評分不低于70分，就表示該用戶對手機“認可”，否則就表示“不認可”，完成下列
列聯表，并回答是否有
的把握認為性別對手機的“認可”有關：
女性用戶 | 男性用戶 | 合計 | |
“認可”手機 | |||
“不認可”手機 | |||
合計 |
附：
| 0.05 | 0.01 |
| 3.841 | 6635 |
（2）根據評分的不同，運用分層抽樣從男性用戶中抽取20名用戶，在這20名用戶中，從評分不低于80分的用戶中任意抽取3名用戶，求3名用戶中評分小于90分的人數的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=x2-4|x|-5．
（Ⅰ）畫出y=f（x）的圖象；
（Ⅱ）設A={x|f（x）≥7}，求集合A；
（Ⅲ）方程f（x）=k+1有兩解，求實數k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
