
【題目】有下列命題:①邊長(zhǎng)為1的正四面體的內(nèi)切球半徑為![]() ;
;
②正方體的內(nèi)切球、棱切球(正方體的每條棱都與球相切)、外接球的半徑之比為1:![]() ;
;
③棱長(zhǎng)為1的正方體ABCD-A1B1C1D1的內(nèi)切球被平面A1BD截得的截面面積為![]() .
.
其中正確命題的序號(hào)是______(請(qǐng)?zhí)钏姓_命題的序號(hào));
【答案】①②③
【解析】
運(yùn)用正四面體的性質(zhì)和體積公式,結(jié)合等積法可得球的半徑,可判斷①;
由正方體與內(nèi)切球、棱切球和外接球的關(guān)系,求得半徑,可判斷②;
求得正方體內(nèi)切球半徑,結(jié)合球的截面性質(zhì),以及勾股定理和等邊三角形的性質(zhì),即可判斷③.
①邊長(zhǎng)為1的正四面體的高為h![]() ,
,
可得正四面體的體積為V![]()
![]() h
h![]() ,
,
設(shè)內(nèi)切球的半徑為r,由等積法可得V![]() rS
rS![]() r4
r4![]() ,(S為正四面體的全面積)
,(S為正四面體的全面積)
解得r![]() ,故①正確;
,故①正確;
②設(shè)邊長(zhǎng)為1的正方體的內(nèi)切球、棱切球(正方體的每條棱都與球相切)、外接球的半徑
分別為r1,r2,r3,可得2r1=1,2r2![]() ,2r3
,2r3![]() ,
,
即有r1:r2:r3=1:![]() ,故②正確;
,故②正確;
③棱長(zhǎng)為1的正方體ABCD﹣A1B1C1D1的內(nèi)切球的半徑為![]() ,
,
設(shè)內(nèi)心為I,可得A1I![]() ,I在截面的射影為等邊三角形A1BD的中心O,
,I在截面的射影為等邊三角形A1BD的中心O,
可得OI![]() ,
,
由球的截面的性質(zhì)可得截面圓的半徑為![]() ,可得截面圓的面積為
,可得截面圓的面積為![]() ,故③正確.
,故③正確.
故答案為:①②③.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2017年“雙節(jié)”期間,高速公路車輛較多.某調(diào)查公司在一服務(wù)區(qū)從七座以下小型汽車中按進(jìn)服務(wù)區(qū)的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進(jìn)行詢問(wèn)調(diào)查,將他們?cè)谀扯胃咚俟返能囁?/span>![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖的頻率分布直方圖.
后得到如圖的頻率分布直方圖.

(1)調(diào)查公司在采樣中,用到的是什么抽樣方法?
(2)求這40輛小型車輛車速的眾數(shù)、中位數(shù)及平均數(shù)的估計(jì)值;
(3)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛至少有一輛的概率.
的車輛至少有一輛的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(Ⅰ)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值;
上的最大值與最小值;
(Ⅱ)當(dāng)![]() 的圖像經(jīng)過(guò)點(diǎn)
的圖像經(jīng)過(guò)點(diǎn)![]() 時(shí),求
時(shí),求![]() 的值及函數(shù)
的值及函數(shù)![]() 的最小正周期.
的最小正周期.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,平面中兩條直線![]() 和
和![]() 相交于點(diǎn)O,對(duì)于平面上任意一點(diǎn)M,若p,q分別是M到直線
相交于點(diǎn)O,對(duì)于平面上任意一點(diǎn)M,若p,q分別是M到直線![]() 和
和![]() 的距離,則稱有序非負(fù)實(shí)數(shù)對(duì)
的距離,則稱有序非負(fù)實(shí)數(shù)對(duì)![]() 是點(diǎn)M的“距離坐標(biāo)”.下列四個(gè)命題中正確命題為( )
是點(diǎn)M的“距離坐標(biāo)”.下列四個(gè)命題中正確命題為( )

A.若![]() ,則“距離坐標(biāo)”為
,則“距離坐標(biāo)”為![]() 的點(diǎn)有且僅有1個(gè)
的點(diǎn)有且僅有1個(gè)
B.若![]() ,且
,且![]() ,則“距離坐標(biāo)”為
,則“距離坐標(biāo)”為![]() 的點(diǎn)有且僅有2個(gè)
的點(diǎn)有且僅有2個(gè)
C.若![]() ,則“距離坐標(biāo)”為
,則“距離坐標(biāo)”為![]() 的點(diǎn)有且僅有4個(gè)
的點(diǎn)有且僅有4個(gè)
D.若![]() ,則點(diǎn)M在一條過(guò)點(diǎn)O的直線上
,則點(diǎn)M在一條過(guò)點(diǎn)O的直線上
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知等腰直角三角形![]() 的斜邊
的斜邊![]() 所在直線方程為
所在直線方程為![]() ,其中
,其中![]() 點(diǎn)在
點(diǎn)在![]() 點(diǎn)上方,直角頂點(diǎn)
點(diǎn)上方,直角頂點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.

(1)求![]() 邊上的高線
邊上的高線![]() 所在直線的方程;
所在直線的方程;
(2)求等腰直角三角形![]() 的外接圓的標(biāo)準(zhǔn)方程;
的外接圓的標(biāo)準(zhǔn)方程;
(3)分別求兩直角邊![]() ,
,![]() 所在直線的方程.
所在直線的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知![]() 是
是![]() 中
中![]() 的角平分線,交
的角平分線,交![]() 邊于點(diǎn)
邊于點(diǎn)![]() .
.
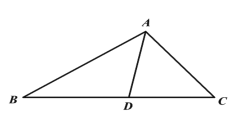
(1)用正弦定理證明: ![]() ;
;
(2)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知在平面直角坐標(biāo)系中,直線l過(guò)點(diǎn)P(1,2).
(1)若直線l在x軸和y軸上的截距相等,求直線l的方程;
(2)求坐標(biāo)原點(diǎn)O到直線l距離取最大值時(shí)的直線l的方程;
(3)設(shè)直線l與x軸正半軸、y軸正半軸分別相交于A,B兩點(diǎn),當(dāng)|PA||PB|最小時(shí),求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是邊長(zhǎng)為2的等邊三角形,點(diǎn)O為AC中點(diǎn),平面AA1C1C⊥平面ABC.

(1)證明:A1O⊥平面ABC;
(2)求直線AB與平面A1BC1所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為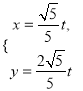 (
(![]() 為參數(shù)),以平面直角坐標(biāo)系的原點(diǎn)為極點(diǎn),正半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線
為參數(shù)),以平面直角坐標(biāo)系的原點(diǎn)為極點(diǎn),正半軸為極軸,取相同的長(zhǎng)度單位建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 和曲線
和曲線![]() 的直角坐標(biāo)方程,并指明曲線
的直角坐標(biāo)方程,并指明曲線![]() 的形狀;
的形狀;
(2)設(shè)直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn), ![]() 為坐標(biāo)原點(diǎn),且
為坐標(biāo)原點(diǎn),且![]() ,求
,求![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com