
【題目】在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() ,側(cè)面
,側(cè)面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
(Ⅰ)求證:直線![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 為
為![]() 的中點,求平面
的中點,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值;
所成銳二面角的余弦值;
(Ⅲ)設(shè)![]() ,當(dāng)
,當(dāng)![]() 為何值時,直線
為何值時,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)見證明;(Ⅱ) ![]() (Ⅲ)
(Ⅲ) ![]()
【解析】
(Ⅰ)因為![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() 。又由題意可知
。又由題意可知![]() 底面
底面![]() ,所以
,所以![]() ,由線面垂直的判定定理即可得證。
,由線面垂直的判定定理即可得證。
(Ⅱ)分別以![]() 為
為![]() 軸、
軸、![]() 軸和
軸和![]() 軸正方向建系,利用向量法能求出平面
軸正方向建系,利用向量法能求出平面![]() 與平面
與平面![]() 所成銳二面角的余弦值。
所成銳二面角的余弦值。
(Ⅲ)由![]() 結(jié)合(2),可得
結(jié)合(2),可得![]() ,
,![]() ,又平面
,又平面![]() ,根據(jù)線面角的余弦值即可求解。
,根據(jù)線面角的余弦值即可求解。
(Ⅰ)證明:在平行四邊形![]() 中,因為
中,因為![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() .
.
因為側(cè)面![]() 底面
底面![]() ,且
,且![]() ,面
,面![]() 面
面![]()
且![]() 面
面![]() 所以
所以![]() 底面
底面![]() .
.
又因為![]() 底面
底面![]() ,所以
,所以![]() .
.
又因為![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)解:因為![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 兩兩垂直,故以
兩兩垂直,故以![]() 分別為
分別為![]() 軸、
軸、![]() 軸和
軸和![]() 軸,建立空間直角坐標(biāo)系,
軸,建立空間直角坐標(biāo)系,
則![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
由![]() ,
,![]() ,得
,得![]()
令![]() ,得
,得![]() .
.
![]() 為
為![]() 的中點,由(1)知,
的中點,由(1)知,![]() 平面
平面![]() 且
且![]() ,
,
所以![]()
![]() ,
,
平面![]() 與平面
與平面![]() 所成銳二面角的余弦值
所成銳二面角的余弦值![]() ;
;
(Ⅲ)設(shè)![]() ,則
,則![]() ,所以
,所以![]() ,
,
![]()
由(1)知![]() .直線
.直線![]() 與平面
與平面![]() 所成的角正弦值為
所成的角正弦值為![]()
所以![]() ,即
,即![]() ,
,
解得![]() .或
.或![]() (舍)
(舍)


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某縣畜牧技術(shù)員張三和李四9年來一直對該縣山羊養(yǎng)殖業(yè)的規(guī)模進(jìn)行跟蹤調(diào)查,張三提供了該縣某山羊養(yǎng)殖場年養(yǎng)殖數(shù)量![]() 單位:萬只
單位:萬只![]() 與相應(yīng)年份
與相應(yīng)年份![]() 序號
序號![]() 的數(shù)據(jù)表和散點圖
的數(shù)據(jù)表和散點圖![]() 如圖所示
如圖所示![]() ,根據(jù)散點圖,發(fā)現(xiàn)y與x有較強的線性相關(guān)關(guān)系,李四提供了該縣山羊養(yǎng)殖場的個數(shù)
,根據(jù)散點圖,發(fā)現(xiàn)y與x有較強的線性相關(guān)關(guān)系,李四提供了該縣山羊養(yǎng)殖場的個數(shù)![]() 單位:個
單位:個![]() 關(guān)于x的回歸方程
關(guān)于x的回歸方程![]() .
.
年份序號x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年養(yǎng)殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根據(jù)表中的數(shù)據(jù)和所給統(tǒng)計量,求y關(guān)于x的線性回歸方程
根據(jù)表中的數(shù)據(jù)和所給統(tǒng)計量,求y關(guān)于x的線性回歸方程![]() 參考統(tǒng)計量:
參考統(tǒng)計量:![]() ,
,![]() ;
;
![]() 試估計:
試估計:![]() 該縣第一年養(yǎng)殖山羊多少萬只
該縣第一年養(yǎng)殖山羊多少萬只
![]() 到第幾年,該縣山羊養(yǎng)殖的數(shù)量與第一年相比縮小了?
到第幾年,該縣山羊養(yǎng)殖的數(shù)量與第一年相比縮小了?
附:對于一組數(shù)據(jù)![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() :
:![]() 的上頂點為
的上頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,點
,點![]() ,
,![]() 在橢圓
在橢圓![]() 上,其中
上,其中![]() 是橢圓上一動點,
是橢圓上一動點,![]() 點坐標(biāo)為
點坐標(biāo)為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)作直線![]() 與
與![]() 軸垂直,交橢圓于
軸垂直,交橢圓于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 兩點均不與
兩點均不與![]() 點重合),直線
點重合),直線![]() ,
,![]() 與
與![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,試求
,試求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某食品廠為了檢查甲乙兩條自動包裝流水線的生產(chǎn)情況,隨機在這兩條流水線上各抽取40件產(chǎn)品作為樣本稱出它們的質(zhì)量(單位:克),質(zhì)量值落在(495,510]的產(chǎn)品為合格品,否則為不合格品.表是甲流水線樣本頻數(shù)分布表,圖是乙流水線樣本頻率分布直方圖.

表甲流水線樣本頻數(shù)分布表
產(chǎn)品質(zhì)量/克 | 頻數(shù) |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |
(1)若以頻率作為概率,試估計從兩條流水線分別任取1件產(chǎn)品,該產(chǎn)品恰好是合格品的概率分別是多少;
(2)由以上統(tǒng)計數(shù)據(jù)作出2×2列聯(lián)表,并回答能否有95%的把握認(rèn)為“產(chǎn)品的包裝質(zhì)量與兩條自動包裝流水線的選擇有關(guān)”
χ2![]()
甲流水線 | 乙流水線 | 總計 | |
合格品 | |||
不合格品 | |||
總計 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】5名運動員參加一次乒乓球比賽,每![]() 名運動員都賽
名運動員都賽![]() 場并決出勝負(fù).設(shè)第
場并決出勝負(fù).設(shè)第![]() 位運動員共勝
位運動員共勝![]() 場,負(fù)
場,負(fù)![]() 場(
場(![]() ),則錯誤的結(jié)論是( )
),則錯誤的結(jié)論是( )
A. ![]()
B. ![]()
C. ![]() 為定值,與各場比賽的結(jié)果無關(guān)
為定值,與各場比賽的結(jié)果無關(guān)
D. ![]() 為定值,與各場比賽結(jié)果無關(guān)
為定值,與各場比賽結(jié)果無關(guān)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 分別為
分別為![]() 的三內(nèi)角A,B,C的對邊,其面積
的三內(nèi)角A,B,C的對邊,其面積![]() ,在等差數(shù)列
,在等差數(shù)列![]() 中,
中,![]() ,公差
,公差![]() .?dāng)?shù)列
.?dāng)?shù)列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() ,求數(shù)列
,求數(shù)列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法:①若線性回歸方程為![]() ,則當(dāng)變量
,則當(dāng)變量![]() 增加一個單位時,
增加一個單位時,![]() 一定增加3個單位;②將一組數(shù)據(jù)中的每個數(shù)據(jù)都加上同一個常數(shù)后,方差不會改變;③線性回歸直線方程
一定增加3個單位;②將一組數(shù)據(jù)中的每個數(shù)據(jù)都加上同一個常數(shù)后,方差不會改變;③線性回歸直線方程![]() 必過點
必過點![]() ;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若對于區(qū)間
,若對于區(qū)間![]() 上的任意
上的任意![]() ,都有
,都有![]() ,則實數(shù)
,則實數(shù)![]() 的最小值是( )
的最小值是( )
A. 20B. 18
C. 3D. 0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年4月,甲乙兩校的學(xué)生參加了某考試機構(gòu)舉行的大聯(lián)考,現(xiàn)從這兩校參加考試的學(xué)生數(shù)學(xué)成績在100分及以上的試卷中用系統(tǒng)抽樣的方法各抽取了20份試卷,并將這40份試卷的得分制作成如下的莖葉圖.
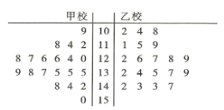
(1)試通過莖葉圖比較這40份試卷的兩校學(xué)生數(shù)學(xué)成績的中位數(shù);
(2)若把數(shù)學(xué)成績不低于135分的記作數(shù)學(xué)成績優(yōu)秀,根據(jù)莖葉圖中的數(shù)據(jù),判斷是否有90![]() 的把握認(rèn)為數(shù)學(xué)成績在100分及以上的學(xué)生中數(shù)學(xué)成績是否優(yōu)秀與所在學(xué)校有關(guān);
的把握認(rèn)為數(shù)學(xué)成績在100分及以上的學(xué)生中數(shù)學(xué)成績是否優(yōu)秀與所在學(xué)校有關(guān);
(3)若從這40名學(xué)生中選取數(shù)學(xué)成績在![]() 的學(xué)生,用分層抽樣的方式從甲乙兩校中抽取5人,再從這5人中隨機抽取3人分析其失分原因,求這3人中恰有2人是乙校學(xué)生的概率.
的學(xué)生,用分層抽樣的方式從甲乙兩校中抽取5人,再從這5人中隨機抽取3人分析其失分原因,求這3人中恰有2人是乙校學(xué)生的概率.
參考公式與臨界值表: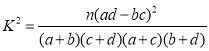 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com