
【題目】在數(shù)列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求證:數(shù)列{an+n}為等比數(shù)列;
(2)記bn=an+(1﹣λ)n,且數(shù)列{bn}的前n項(xiàng)和為Tn , 若T3為數(shù)列{Tn}中的最小項(xiàng),求λ的取值范圍.
【答案】
(1)證明:∵an+1=3an+2n﹣1,
∴an+1+n+1=3(an+n).
又a1=2,
∴an>0,an+n>0,
故 ![]() ,
,
∴{an+n}是以3為首項(xiàng),公比為3的等比數(shù)列
(2)由(1)知道 ![]() ,bn=an+(1﹣λ)n,
,bn=an+(1﹣λ)n,
∴ ![]() .
.
∴ ![]() .
.
若T3為數(shù)列{Tn}中的最小項(xiàng),則對n∈N*有 ![]() 恒成立,
恒成立,
即3n+1﹣81≥(n2+n﹣12)λ對n∈N*恒成立
1°當(dāng)n=1時(shí),有 ![]() ;
;
2°當(dāng)n=2時(shí),有T2≥T3λ≥9;
3°當(dāng)n≥4時(shí),n2+n﹣12=(n+4)(n﹣3)>0恒成立,
∴ ![]() 對n≥4恒成立.
對n≥4恒成立.
令 ![]() ,則
,則 ![]() 對n≥4恒成立,
對n≥4恒成立,
∴ ![]() 在n≥4時(shí)為單調(diào)遞增數(shù)列.
在n≥4時(shí)為單調(diào)遞增數(shù)列.
∴λ≤f(4),即 ![]() .
.
綜上, ![]()
【解析】(1)由an+1=3an+2n﹣1,整理得:an+1+n+1=3(an+n).由an+n>0, ![]() ,可知{an+n}是以3為首項(xiàng),公比為3的等比數(shù)列;(2)由(1)求得數(shù)列{bn}通項(xiàng)公式及前n項(xiàng)和為Tn , 由T3為數(shù)列{Tn}中的最小項(xiàng),則對n∈N*有
,可知{an+n}是以3為首項(xiàng),公比為3的等比數(shù)列;(2)由(1)求得數(shù)列{bn}通項(xiàng)公式及前n項(xiàng)和為Tn , 由T3為數(shù)列{Tn}中的最小項(xiàng),則對n∈N*有 ![]() 恒成立,分類分別求得當(dāng)n=1時(shí)和當(dāng)n=2λ的取值范圍, 當(dāng)n≥4時(shí),
恒成立,分類分別求得當(dāng)n=1時(shí)和當(dāng)n=2λ的取值范圍, 當(dāng)n≥4時(shí), ![]() ,利用做差法,根據(jù)函數(shù)的單調(diào)性,即可求得λ的取值范圍.
,利用做差法,根據(jù)函數(shù)的單調(diào)性,即可求得λ的取值范圍.
【考點(diǎn)精析】關(guān)于本題考查的數(shù)列的前n項(xiàng)和和數(shù)列的通項(xiàng)公式,需要了解數(shù)列{an}的前n項(xiàng)和sn與通項(xiàng)an的關(guān)系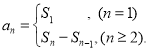 ;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項(xiàng)公式才能得出正確答案.
;如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項(xiàng)公式才能得出正確答案.


 贏在課堂名師課時(shí)計(jì)劃系列答案
贏在課堂名師課時(shí)計(jì)劃系列答案 天天向上課時(shí)同步訓(xùn)練系列答案
天天向上課時(shí)同步訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l:x+2y-2=0.試求:
(1)點(diǎn)P(-2,-1)關(guān)于直線l的對稱點(diǎn)坐標(biāo);
(2)直線l關(guān)于點(diǎn)(1,1)對稱的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (a為常數(shù))的圖象與
(a為常數(shù))的圖象與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為
處的切線斜率為![]()
(1)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的極值;
的極值;
(2)證明:當(dāng)![]() 時(shí),
時(shí),![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結(jié)果揭曉前,甲、乙、丙、丁四位同學(xué)對這四件參賽作品的獲獎情況預(yù)測如下:
四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結(jié)果揭曉前,甲、乙、丙、丁四位同學(xué)對這四件參賽作品的獲獎情況預(yù)測如下:
甲說:“![]() 、
、![]() 同時(shí)獲獎”;
同時(shí)獲獎”;
乙說:“![]() 、
、![]() 不可能同時(shí)獲獎”;
不可能同時(shí)獲獎”;
丙說:“![]() 獲獎”;
獲獎”;
丁說:“![]() 、
、![]() 至少一件獲獎”.
至少一件獲獎”.
如果以上四位同學(xué)中有且只有二位同學(xué)的預(yù)測是正確的,則獲獎的作品是( )
A. 作品![]() 與作品
與作品![]() B. 作品
B. 作品![]() 與作品
與作品![]() C. 作品
C. 作品![]() 與作品
與作品![]() D. 作品
D. 作品![]() 與作品
與作品![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知立方和公式:![]()
![]() 求函數(shù)
求函數(shù)![]() 的值域;
的值域;
![]() 求函數(shù)
求函數(shù)![]() ,
,![]() 的值域;
的值域;
![]() 若任意實(shí)數(shù)x,不等式
若任意實(shí)數(shù)x,不等式![]() 恒成立,求實(shí)數(shù)a的取值范圍.
恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在下列命題中,①![]() 的一個充要條件是
的一個充要條件是![]() 與它的共軛復(fù)數(shù)相等:
與它的共軛復(fù)數(shù)相等:
②利用獨(dú)立性檢驗(yàn)來考查兩個分類變量![]() ,
,![]() 是否有關(guān)系,當(dāng)隨機(jī)變量
是否有關(guān)系,當(dāng)隨機(jī)變量![]() 的觀測值
的觀測值![]() 值越大,“
值越大,“![]() 與
與![]() 有關(guān)系”成立的可能性越大;
有關(guān)系”成立的可能性越大;
③在回歸分析模型中,若相關(guān)指數(shù)越大,則殘差平方和越小,模型的擬合效果越好;
④若![]() ,
,![]() 是兩個相等的實(shí)數(shù),則
是兩個相等的實(shí)數(shù),則![]() 是純虛數(shù);
是純虛數(shù);
⑤某校高三共有![]() 個班,
個班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推測各班都超過
人,由此推測各班都超過![]() 人,這個推理過程是演繹推理.
人,這個推理過程是演繹推理.
其中真命題的序號為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國家質(zhì)量監(jiān)督檢驗(yàn)檢疫局于2004年5月31日發(fā)布了新的![]() 車輛駕駛?cè)藛T血液、呼氣酒精含量閥值與檢驗(yàn)
車輛駕駛?cè)藛T血液、呼氣酒精含量閥值與檢驗(yàn)![]() 國家標(biāo)準(zhǔn)
國家標(biāo)準(zhǔn)![]() 新標(biāo)準(zhǔn)規(guī)定,車輛駕駛?cè)藛T血液中的酒精含量大于或等于20毫克
新標(biāo)準(zhǔn)規(guī)定,車輛駕駛?cè)藛T血液中的酒精含量大于或等于20毫克![]() 百毫升,小于80毫克
百毫升,小于80毫克![]() 百毫升為飲酒駕車,血液中的酒精含量大于或等于80毫克
百毫升為飲酒駕車,血液中的酒精含量大于或等于80毫克![]() 百毫升為醉酒駕車
百毫升為醉酒駕車![]() 經(jīng)過反復(fù)試驗(yàn),喝一瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點(diǎn)圖”如圖:
經(jīng)過反復(fù)試驗(yàn),喝一瓶啤酒后酒精在人體血液中的變化規(guī)律的“散點(diǎn)圖”如圖:

該函數(shù)近似模型如下: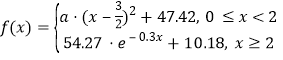 ,又已知剛好過1小時(shí)時(shí)測得酒精含量值為
,又已知剛好過1小時(shí)時(shí)測得酒精含量值為![]() 毫克
毫克![]() 百毫升
百毫升![]() 根據(jù)上述條件,回答以下問題:
根據(jù)上述條件,回答以下問題:
![]() 試計(jì)算喝1瓶啤酒多少小時(shí)血液中的酒精含量達(dá)到最大值?最大值是多少?
試計(jì)算喝1瓶啤酒多少小時(shí)血液中的酒精含量達(dá)到最大值?最大值是多少?
![]() 試計(jì)算喝一瓶啤酒后多少小時(shí)后才可以駕車?
試計(jì)算喝一瓶啤酒后多少小時(shí)后才可以駕車?![]() 時(shí)間以整小時(shí)計(jì)算
時(shí)間以整小時(shí)計(jì)算![]()
![]() 參考數(shù)據(jù):
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為研究某藥品的療效,選取若干名志愿者進(jìn)行臨床試驗(yàn),所有志愿者的舒張壓數(shù)據(jù)(單位:![]() )的分組區(qū)間為
)的分組區(qū)間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據(jù)試驗(yàn)數(shù)據(jù)制成的頻率分布直方圖.已知第一組與第二組共有
,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據(jù)試驗(yàn)數(shù)據(jù)制成的頻率分布直方圖.已知第一組與第二組共有![]() 人,第三組中沒有療效的有
人,第三組中沒有療效的有![]() 人,則第三組中有療效的人數(shù)為( )
人,則第三組中有療效的人數(shù)為( )
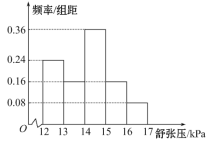
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com