【題目】越接近高考學生焦慮程度越強，四個高三學生中大約有一個有焦慮癥，經有關機構調查，得出距離高考周數與焦慮程度對應的正常值變化情況如下表：
周數x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散點圖：
(2)根據上表數據用最小二乘法求出y關于x的線性回歸方程 (精確到0.01)；
(3)根據經驗，觀測值為正常值的0.85～1.06為正常，若1.06～1.12為輕度焦慮，1.12～1.20為中度焦慮，1.20及其以上為重度焦慮，若為中度焦慮及其以上，則要進行心理疏導，若一個學生在距高考第二周時觀測值為100，則該學生是否需要進行心理疏導？
（
, 
）
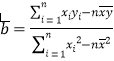科目：高中數學 來源： 題型：
【題目】已知函數
是定義在
上的偶函數，當
時，
．現已畫出函數在
軸右側的圖象，如圖所示．
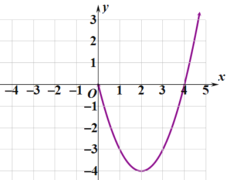
（1）畫出函數在軸左側的圖象，根據圖象寫出函數在上的單調區間；
（2）求函數在上的解析式；
（3）解不等式
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知對任意平面向量
，把
繞其起點沿逆時針方向旋轉
角得到向量
，叫做把點
繞點
逆時針方向旋轉角得到點
.
（1）已知平面內點
，點
.把點繞點沿順時針方向旋轉
后得到點，求點的坐標；
（2）設平面內曲線
上的每一點繞坐標原點沿逆時針方向旋轉后得到的點的軌跡是曲線
，求原來曲線的方程，并求曲線上的點到原點距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】手機作為客戶端越來越為人們所青睞，通過手機實現衣食住行消費已經成為一種主要的消費方式.在某市，隨機調查了200名顧客購物時使用手機支付的情況，得到如下的2×2列聯表，已知從使用手機支付的人群中隨機抽取1人，抽到青年的概率為
.
（I）根據已知條件完成2×2列聯表，并根據此資料判斷是否有99.5%的把握認為“市場購物用手機支付與年齡有關”？
2×2列聯表：
青年 | 中老年 | 合計 | |
使用手機支付 | 120 | ||
不使用手機支付 | 48 | ||
合計 | 200 |
（Ⅱ）現采用分層抽樣的方法從這200名顧客中按照“使用手機支付”和“不使用手機支付”抽取一個容量為10的樣本，再從中隨機抽取3人，求這三人中“使用手機支付”的人數的分布列及期望.
附：
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將參加夏令營的400名學生編號為：001，002，…，400，采用系統抽樣的方法抽取一個容量為40的樣本，且隨機抽得的號碼為003，這400名學生分住在三個營區，從001到180在第一營區，從181到295在第二營區，從296到400在第三營區，三個營區被抽中的人數分別為( )
A. 18，12，10 B. 20，12，8 C. 17，13，10 D. 18，11，11
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
過點
，離心率為
，
為坐標原點.
（1）求橢圓
的標準方程；
（2）設
，
，
為橢圓上的三點，
與
交于點
，且
，當的中點恰為點時，判斷
的面積是否為常數，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
