
【題目】已知對任意平面向量![]() ,把
,把![]() 繞其起點沿逆時針方向旋轉
繞其起點沿逆時針方向旋轉![]() 角得到向量
角得到向量![]() ,叫做把點
,叫做把點![]() 繞點
繞點![]() 逆時針方向旋轉
逆時針方向旋轉![]() 角得到點
角得到點![]() .
.
(1)已知平面內點![]() ,點
,點![]() .把點
.把點![]() 繞點
繞點![]() 沿順時針方向旋轉
沿順時針方向旋轉![]() 后得到點
后得到點![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)設平面內曲線![]() 上的每一點繞坐標原點沿逆時針方向旋轉
上的每一點繞坐標原點沿逆時針方向旋轉![]() 后得到的點的軌跡是曲線
后得到的點的軌跡是曲線![]() ,求原來曲線
,求原來曲線![]() 的方程,并求曲線
的方程,并求曲線![]() 上的點到原點距離的最小值.
上的點到原點距離的最小值.
【答案】(1)![]() (2)
(2)![]() ;
;![]()
【解析】
![]() 設
設![]() 則
則![]() ,
,![]() ,根據題意, 點
,根據題意, 點![]() 繞點
繞點![]() 沿順時針方向旋轉
沿順時針方向旋轉![]() ,利用
,利用![]() 代入公式求解即可;
代入公式求解即可;
![]() 設
設![]() 是曲線
是曲線![]() 上任一點,
上任一點,![]() 是點
是點![]() 繞坐標原點沿逆時針方向旋轉
繞坐標原點沿逆時針方向旋轉![]() 后得到的曲線
后得到的曲線![]() 上的點,則
上的點,則![]() ,
,![]() ,代入題中的公式,列出
,代入題中的公式,列出![]() 與
與![]() 的關系式,利用相關點法求出曲線
的關系式,利用相關點法求出曲線![]() 的方程,由兩點間距離公式表示出
的方程,由兩點間距離公式表示出![]() ,令
,令![]() ,考慮函數
,考慮函數![]() ,通過構造對勾函數
,通過構造對勾函數![]() 并判斷其單調性求出最小值即可求出
并判斷其單調性求出最小值即可求出![]() 的最小值.
的最小值.
(1)由題意知,![]() ,設
,設![]() ,則
,則![]() ,
,
由條件得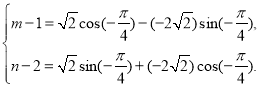
解之得![]() ,∴
,∴![]() .
.
(2)設![]() 是曲線
是曲線![]() 上任一點,
上任一點,![]() 是點
是點![]() 繞坐標原點
繞坐標原點
沿逆時針方向旋轉![]() 后得到的曲線
后得到的曲線![]() 上的點,
上的點,
所以![]() ,
,![]() ,
,
則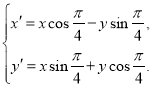 ,即
,即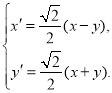
又![]() 在曲線
在曲線![]() 上,所以
上,所以![]() ,
,
即![]() ,整理得
,整理得![]() ,
,
故曲線![]() 的方程是
的方程是![]() ,
,
所以曲線C上的點![]() 到原點的距離為
到原點的距離為![]() ,
,
令![]() ,則
,則![]() ,考慮函數
,考慮函數![]() ,
,
任取![]() 且
且![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上單調遞減,
上單調遞減,
同理可證![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() .
.
故![]() ,即曲線
,即曲線![]() 上的點到原點距離的最小值為
上的點到原點距離的最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】(1)6個人按下列要求站一橫排,甲、乙必須相鄰,有多少種不同的站法?
(2)6個人按下列要求站一橫排,甲不站左端,乙不站右端.有多少種不同的站法?
(3)用0,1,2,3,4,5這六個數字可以組成多少個六位數且是奇數(無重復數字的數)?
(4)用0,1,2,3,4,5這六個數字可以組成多少個個位上的數字不是5的六位數(無重復數字的數)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如表提供了工廠技術改造后某種型號設備的使用年限![]() 和所支出的維修費
和所支出的維修費![]() (萬元)的幾組對照數據:
(萬元)的幾組對照數據:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
參考公式: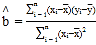 ,
,![]() .
.
(1)若知道![]() 對
對![]() 呈線性相關關系,請根據上表提供的數據,用最小二乘法求出
呈線性相關關系,請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該工廠技術改造前該型號設備使用10年的維修費用為9萬元,試根據(1)求出的線性回歸方程,預測該型號設備技術改造后,使用10年的維修費用能否比技術改造前降低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知過點![]() 的圓
的圓![]() 和直線
和直線![]() 相切,且圓心在直線
相切,且圓心在直線![]() 上.
上.
(1)求圓![]() 的標準方程;
的標準方程;
(2)點![]() ,圓
,圓![]() 上是否存在點
上是否存在點![]() ,使
,使![]()
![]() 若存在,求出點
若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】越接近高考學生焦慮程度越強,四個高三學生中大約有一個有焦慮癥,經有關機構調查,得出距離高考周數與焦慮程度對應的正常值變化情況如下表:
周數x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散點圖:

(2)根據上表數據用最小二乘法求出y關于x的線性回歸方程 (精確到0.01);
(3)根據經驗,觀測值為正常值的0.85~1.06為正常,若1.06~1.12為輕度焦慮,1.12~1.20為中度焦慮,1.20及其以上為重度焦慮,若為中度焦慮及其以上,則要進行心理疏導,若一個學生在距高考第二周時觀測值為100,則該學生是否需要進行心理疏導?
(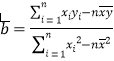 ,
, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com