
【題目】某高校數學與統計學院為了對2018年錄取的大一新生有針對性地進行教學.從大一新生中隨機抽取40名,對他們在2018年高考的數學成績進行調查,統計發現40名新生的數學分數![]() 分布在
分布在![]() 內.當
內.當![]() 時,其頻率
時,其頻率![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)請在答題卡中畫出這40名新生高考數學分數的頻率分布直方圖,并估計這40名新生的高考數學分數的平均數;

(Ⅲ)從成績在100~120分的學生中,用分層抽樣的方法從中抽取5名學生,再從這5名學生中隨機選兩人甲、乙,記甲、乙的成績分別為![]() ,求概率
,求概率![]() .
.
【答案】(Ⅰ)a=0.04;(Ⅱ)見解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)分別取n的值,將n代入函數的解析式,得到關于a的方程,解出即可;
(Ⅱ)畫出頻率分布直方圖,求出平均數即可;
(Ⅲ)按分層抽樣的方法從成績在100~120分的學生中,抽取[100,110)內2人,[110,120)內3人,記[100,110)內2人為A,B,[110,120)內3人,為a,b,c,從而求出滿足條件的概率即可.
(Ⅰ)由題意知,n的取值為10,11,12,13,14.
把n的取值分別代入![]() ,
,
可得(0.5﹣10a)+(0.55﹣10a)+(0.6﹣10a)+(0.65﹣10a)+(0.7﹣10a)=1.
解得a=0.04.
(Ⅱ)頻率分布直方圖如圖:
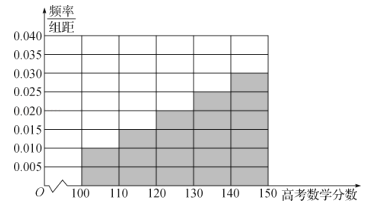
這40名新生的高考數學分數的平均數為105×0.10+115×0.15+125×0.20+135×0.25+145×0.30=130.
(Ⅲ)這40名新生的高考數學分數在[100,110)的頻率為0.1,
分數在[110,120)的頻率為0.15,
頻率比0.1:0.15=2:3.
按分層抽樣的方法從成績在100~120分的學生中,抽取[100,110)內2人,[110,120)內3人,記[100,110)內2人為A,B,[110,120)內3人,為a,b,c.
從5名學生中隨機抽取2名學生的基本事件為AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,共10個,
甲、乙的成績分別為![]() ,滿足
,滿足![]() 的有:Aa,Ab,Ac,Ba,Bb,Bc,共6個.
的有:Aa,Ab,Ac,Ba,Bb,Bc,共6個.
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】
某初級中學共有學生2000名,各年級男、女生人數如下表:
初一年級 | 初二年級 | 初三年級 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校學生中隨機抽取1名,抽到初二年級女生的概率是0.19.
求x的值;
現用分層抽樣的方法在全校抽取48名學生,問應在初三年級抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年級中女生比男生多的概率.
245,求初三年級中女生比男生多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() ,其右焦點為
,其右焦點為![]() .點
.點![]() 是橢圓
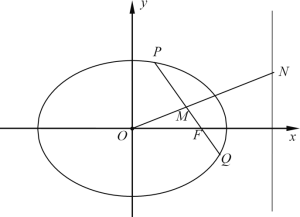
是橢圓![]() 上異于長軸端點的任意一點,連接
上異于長軸端點的任意一點,連接![]() 并延長交橢圓
并延長交橢圓![]() 于點
于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且直線
為坐標原點,且直線![]() 與右準線
與右準線![]() 交于點
交于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(Ⅰ)求橢圓方程;
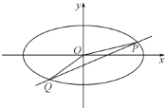
(Ⅱ)設不過原點![]() 的直線
的直線![]() ,與該橢圓交于
,與該橢圓交于![]() 兩點,直線
兩點,直線![]() 的斜率分別為
的斜率分別為![]() ,滿足
,滿足![]() .
.
(i)當![]() 變化時,
變化時,![]() 是否為定值?若是,求出此定值,并證明你的結論;若不是,請說明理由;
是否為定值?若是,求出此定值,并證明你的結論;若不是,請說明理由;
(ii)求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 與
與![]() 的交點的軌跡
的交點的軌跡![]() 的方程;
的方程;
(2)若曲線![]() 上存在4個點到直線
上存在4個點到直線![]() 的距離相等,求實數
的距離相等,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com