【題目】已知拋物線
：
上橫坐標為4的點到焦點的距離為5.
（1）求拋物線的方程；
（2）設直線
與拋物線交于兩點
、
，且
，
是弦
中點，過作平行于
軸的直線交拋物線于點
，得到
，再分別過弦
、
的中點作平行于軸的直線依次交拋物線于點
、
，得到
和
，按此方法繼續下去，解決下列問題：
①求證：
；
②計算的面積
；
③根據的面積的計算結果，寫出、的面積，請設計一種求拋物線與線段所圍成封閉圖形面積的方法，并求此封閉圖形的面積.
【答案】（1）
；（2）①見解析； ②
；③
，無窮等比數列各項和.
.
【解析】
（1）由拋物線的定義、結合已知可以直接求出
的值，進而可以求出拋物線的方程；
（2）①：直線方程與拋物線方程聯立，根據根的判別式、根與系數的關系、結合
，可以證明出
；
②：利用中點坐標公式和三角形面積公式直接求解即可；
③：同②可知：
只與有關，于是可知
，
分別與
、
有關，這樣可以求出它們的面積；這樣無限操作下去，每次得到的三角形面積都相等，面積是一個等比數列，每次得到的三角形的個數也是等比數列，利用無窮等比數列前
項和公式，這樣可以求出拋物線
與線段
所圍成封閉圖形面積.
（1）拋物線的準線方程為：
，由拋物線的定義可知：
，所以拋物線的方程為：；
（2）①：聯立直線和拋物線方程得：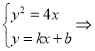
，
∴
，
；
∴
；
②：由中點坐標公式可得：
，∴
，
，
，
；
③：由同②可知：只與有關，而
，
所以
，這樣無限操作下去，第次操作，得到
個小三角形，每個三角形的面積為：
，這無窮多個三角形的面積之和就是拋物線與線段所圍成封閉圖形面積，所以有
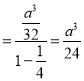
所求的面積為.
春雨教育同步作文系列答案科目：高中數學 來源： 題型：
【題目】2002年在北京召開的國際數學家大會的會標是以我國古代數學家的弦圖為基礎設計的.弦圖是由四個全等的直角三角形與一個小正方形拼成的一個大正方形（如圖）.設其中直角三角形中較小的銳角為
，且
，如果在弦圖內隨機拋擲1000米黑芝麻（大小差別忽略不計），則落在小正方形內的黑芝麻數大約為（ ）
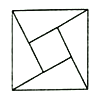
A. 350B. 300C. 250D. 200
查看答案和解析>>
科目：高中數學 來源： 題型：
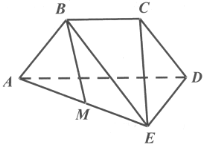
【題目】如圖等腰梯形
中
，且平面 
平面
，
，
為線段
的中點.
（1）求證：直線
平面
；
（2）求證：平面 
平面；
（3）若二面角
的大小為
，求直線
與平面所成角的正切值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某地區2008年至2014年中，每年的居民人均純收入y（單位：千元）的數據如下表：
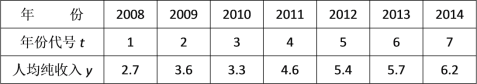
對變量t與y進行相關性檢驗，得知t與y之間具有線性相關關系．
（1）求y關于t的線性回歸方程；
（2）預測該地區2016年的居民人均純收入．
附：回歸直線的斜率和截距的最小二乘估計公式分別為：
，
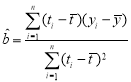查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校從參加某次知識競賽測試得學生中隨機抽取60名學生，將其成績（百分制均為整數）分成6段
，
，…，
后得到如下部分頻率直方分布圖，觀察圖形得信息，回答下列問題：
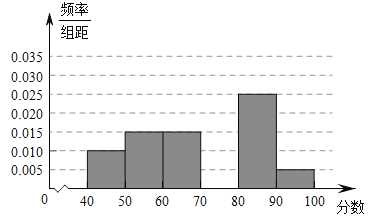
（1）求分數在
內的頻率；
（2）若用樣本估計總體，已知該校參加知識競賽一共有300人，請估計本次考試成績不低于80分的人數；
（3）統計方法中，同一組數據常用該組區間中點值作為代表，據此估計本次考試的平均分.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在
處的切線
與直線
平行.
（1）求實數
的值；
（2）若函數
在
上恰有兩個零點，求實數
的取值范圍.
（3）記函數
，設
是函數
的兩個極值點，若
，且
恒成立，求實數
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
