
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)過點
=1(a>b>0)過點 ![]() ,且離心率e為
,且離心率e為 ![]() .
.
(1)求橢圓E的方程;
(2)設直線x=my﹣1(m∈R)交橢圓E于A,B兩點,判斷點G ![]() 與以線段AB為直徑的圓的位置關系,并說明理由.
與以線段AB為直徑的圓的位置關系,并說明理由.
【答案】
(1)
解:由已知得 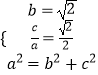 ,解得
,解得 ![]() ,
,
∴橢圓E的方程為 ![]()
(2)
解法一:設點A(x1y1),B(x2,y2),AB中點為H(x0,y0).
由 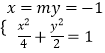 ,化為(m2+2)y2﹣2my﹣3=0,
,化為(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,∴y0=
,∴y0= ![]() .
.
G ![]() ,
,
∴|GH|2= ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() .
.
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故|GH|2﹣ ![]() =
= ![]() +
+ ![]() =
= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() >0.
>0.
∴ ![]() ,故G在以AB為直徑的圓外
,故G在以AB為直徑的圓外
解法二:設點A(x1y1),B(x2,y2),則 ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
由 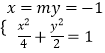 ,化為(m2+2)y2﹣2my﹣3=0,
,化為(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,
,
從而 ![]() =
= ![]()
= ![]() +y1y2
+y1y2
= ![]() +
+ ![]()
= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() >0.
>0.
∴ ![]() >0,又
>0,又 ![]() ,
, ![]() 不共線,
不共線,
∴∠AGB為銳角.
故點G ![]() 在以AB為直徑的圓外
在以AB為直徑的圓外
【解析】解法一:(1)由已知得 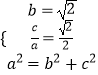 ,解得即可得出橢圓E的方程.(2)設點A(x1 , y1),B(x2 , y2),AB中點為H(x0 , y0).直線方程與橢圓方程聯立化為(m2+2)y2﹣2my﹣3=0,利用根與系數的關系中點坐標公式可得:y0=
,解得即可得出橢圓E的方程.(2)設點A(x1 , y1),B(x2 , y2),AB中點為H(x0 , y0).直線方程與橢圓方程聯立化為(m2+2)y2﹣2my﹣3=0,利用根與系數的關系中點坐標公式可得:y0= ![]() .|GH|2=
.|GH|2= ![]() .
. ![]() =
= ![]() ,作差|GH|2﹣
,作差|GH|2﹣ ![]() 即可判斷出.解法二:(1)同解法一.(2)設點A(x1 , y1),B(x2 , y2),則
即可判斷出.解法二:(1)同解法一.(2)設點A(x1 , y1),B(x2 , y2),則 ![]() =
= ![]() ,
, ![]() =
= ![]() .直線方程與橢圓方程聯立化為(m2+2)y2﹣2my﹣3=0,計算
.直線方程與橢圓方程聯立化為(m2+2)y2﹣2my﹣3=0,計算 ![]() =
= ![]() 即可得出∠AGB,進而判斷出位置關系.
即可得出∠AGB,進而判斷出位置關系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知在長方體ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是側棱BB1的中點,則直線AE與平面A1ED1所成角的大小為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
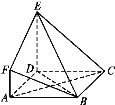
(1)求二面角F-BE-D的余弦值;
(2)設點M是線段BD上一個動點,試確定點M的位置,使得AM∥平面BEF,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,公園內有一塊邊長為![]() 的等邊
的等邊![]() 形狀的三角地,現修成草坪,圖中
形狀的三角地,現修成草坪,圖中![]() 把草坪分成面積相等的兩部分,
把草坪分成面積相等的兩部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(Ⅰ)設![]()
![]() ,試用
,試用![]() 表示
表示![]() 的函數關系式;
的函數關系式;
(Ⅱ)如果![]() 是灌溉水管,為節約成本希望它最短,
是灌溉水管,為節約成本希望它最短,![]() 的位置應該在哪里?如果
的位置應該在哪里?如果![]() 是參觀線路,則希望它最長,
是參觀線路,則希望它最長,![]() 的位置又在哪里?請給予證明.
的位置又在哪里?請給予證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣1|+|x﹣2|
(1)求不等式f(x)≤3的解集;
(2)若不等式||a+b|﹣|a﹣b||≤|a|f(x)(a≠0,a∈R,b∈R)恒成立,求實數x的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{cn}的前n項和為Tn , 若數列{cn}滿足各項均為正項,并且以(cn , Tn)(n∈N*)為坐標的點都在曲線 ![]() 上運動,則稱數列{cn}為“拋物數列”.已知數列{bn}為“拋物數列”,則( )
上運動,則稱數列{cn}為“拋物數列”.已知數列{bn}為“拋物數列”,則( )
A.{bn}一定為等比數列
B.{bn}一定為等差數列
C.{bn}只從第二項起為等比數列
D.{bn}只從第二項起為等差數列
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com