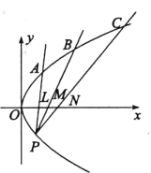
【題目】如圖，已知
為拋物線
上在
軸下方的一點，直線
，
，
與拋物線在第一象限的交點從左到右依次為
，
，
，與軸的正半軸分別相交于點
，
，
，且
，直線的方程為
.
（1）當
時，設直線，的斜率分別為
，
，證明：
；
（2）求
關于
的表達式，并求出的取值范圍.
【答案】(1)見解析.(2) 
.
【解析】
(1)由題意首先確定點P的坐標，然后設出點M,N的坐標，利用斜率公式求得斜率即可證得題中的等式；
(2)由題意首先確定點A和點C的坐標，然后求解點
到直線
的距離和點
到直線的距離，最后結合幾何圖形的性質得到面積比值的函數，由函數的定義域和函數的值域可確定
的取值范圍.
（1）由
解得
或
，則
.
易知
，由題意可得
，
（
，且
），
所以
，
，
所以
，
.
所以
.
（2）由（1）得，當時，直線
的方程為
，
當
時，直線的方程為，適合上式，
所以直線的方程為.
由
消去
得
，
所以
，解得
，所以點的坐標為
.
由（1）得，直線
的方程為
，
由
消去得
，
所以
，解得
，所以點的坐標為
.
則點到直線的距離為
，
點到直線的距離為
，
所以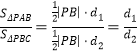
.
因為，所以
，所以
，
所以的取值范圍是
.
科目：高中數學 來源： 題型：
【題目】袋子中有四個小球，分別寫有“美、麗、華、一”四個字，有放回地從中任取一個小球，直到“華”“一”兩個字都取到就停止，用隨機模擬的方法估計恰好在第四次停止的概率．利用計算機隨機產生0到3之間取整數值的隨機數，分別用0，1，2，3代表“美、麗、華、一”這四個字，以每四個隨機數為一組，表示取球四次的結果，經隨機模擬產生了以下20組隨機數：
2323 3211 2303 1233 0211 1322 2201 2213 0012 1231
2312 1300 2331 0312 1223 1031 3020 3223 3301 3212
由此可以估計，恰好第四次就停止的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間進行分析研究，他們分別記錄了12月1日至12月5日的每天晝夜溫差與實驗室每天每100棵種子中的發芽數，得到如下資料：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發芽 | 23 | 25 | 30 | 26 | 16 |
該農科所確定的研究方案是：先從這5組數據中選取3組數據求線性回歸方程，再用剩下的2組數據進行檢驗．
(1)若選取的3組數據恰好是連續
天的數據(
表示數據來自互不相鄰的三天)，求的分布列及期望：
(2)根據12月2日至4日數據，求出發芽數
關于溫差
的線性回歸方程
．由所求得線性回歸方稻得到的估計數據與剩下的檢驗數據的誤差均不超過2顆，則認為得到的線性回歸方程是可靠的，試問所得的線性回歸方程是否可靠？
附：參考公式：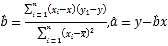
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現在，很多人都喜歡騎“共享單車”，但也有很多市民并不認可．為了調查人們對這種交通方式的認可度，某同學從交通擁堵不嚴重的A城市和交通擁堵嚴重的B城市分別隨機調查了20名市民，得到了一個市民是否認可的樣本，具體數據如下
列聯表：
附：
，
．
根據表中的數據，下列說法中，正確的是（ ）
A. 沒有95% 以上的把握認為“是否認可與城市的擁堵情況有關”
B. 有99% 以上的把握認為“是否認可與城市的擁堵情況有關”
C. 可以在犯錯誤的概率不超過0.01的前提下認為“是否認可與城市的擁堵情況有關”
D. 可以在犯錯誤的概率不超過0.025的前提下認為“是否認可與城市的擁堵情況有關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現代社會，“鼠標手”已成為常見病，一次實驗中，10名實驗對象進行160分鐘的連續鼠標點擊游戲，每位實驗對象完成的游戲關卡一樣，鼠標點擊頻率平均為180次/分鐘，實驗研究人員測試了實驗對象使用鼠標前后的握力變化，前臂表面肌電頻率（
）等指標.
（I）10 名實驗對象實驗前、后握力（單位：
）測試結果如下：
實驗前：346,357,358,360,362,362,364,372,373,376
實驗后：313,321,322,324,330,332,334,343,350,361
完成莖葉圖，并計算實驗后握力平均值比實驗前握力的平均值下降了多少？
（Ⅱ）實驗過程中測得時間
（分）與10名實驗對象前臂表面肌電頻率（）的中的位數
（
）的九組對應數據
為
，
.建立關于時間的線性回歸方程；
（Ⅲ）若肌肉肌電水平顯著下降，提示肌肉明顯進入疲勞狀態，根據（Ⅱ）中9組數據分析，使用鼠標多少分鐘就該進行休息了？
參考數據：
；
參考公式：回歸方程
中斜率和截距的最小二乘估計公式分別為：
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】畫糖是一種以糖為材料在石板上進行造型的民間藝術，常見于公園與旅游景點.某師傅制作了一種新造型糖畫，為了進行合理定價先進性試銷售，其單價
（元）與銷量
（個）相關數據如下表：
（1）已知銷量與單價具有線性相關關系，求關于的線性相關方程；
（2）若該新造型糖畫每個的成本為
元，要使得進入售賣時利潤最大，請利用所求的線性相關關系確定單價應該定為多少元？（結果保留到整數）
參考公式：線性回歸方程
中斜率和截距最小二乘法估計計算公式：
.參考數據：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
