
【題目】如圖點![]() 是半徑為
是半徑為![]() 的砂輪邊緣上的一個質點,它從初始位置
的砂輪邊緣上的一個質點,它從初始位置![]() (
(![]() ,
,![]() )開始,按逆時針方向每
)開始,按逆時針方向每![]() 旋轉一周,
旋轉一周,![]() .
.
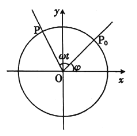
(1)求點![]() 的縱坐標
的縱坐標![]() 關于時間
關于時間![]() 的函數關系;
的函數關系;
(2)求點![]() 的運動周期和頻率;
的運動周期和頻率;
(3)函數![]() 的圖像可由余弦曲線經過怎樣的變化得到?
的圖像可由余弦曲線經過怎樣的變化得到?
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,直線
,直線
![]() 與橢圓
與橢圓![]() 的兩個交點間的距離為
的兩個交點間的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖,過![]() ,
,![]() 作兩條平行線
作兩條平行線![]() ,
,![]() 與橢圓
與橢圓![]() 的上半部分分別交于
的上半部分分別交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形
![]() 面積的最大值.
面積的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.

(1)證明: ![]() ;
;
(2)設![]() 為線段
為線段![]() 上的動點,若線段
上的動點,若線段![]() 長的最小值為
長的最小值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)證明線線垂直則需證明線面垂直,根據題意易得![]() ,然后根據等邊三角形的性質可得
,然后根據等邊三角形的性質可得![]() ,又
,又![]() ,因此
,因此![]() 得
得![]() 平面
平面![]() ,從而得證(2)先找到EH什么時候最短,顯然當線段
,從而得證(2)先找到EH什么時候最短,顯然當線段![]() 長的最小時,
長的最小時, ![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,由
,由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .然后建立空間直角坐標系,寫出兩個面法向量再根據向量的夾角公式即可得余弦值
.然后建立空間直角坐標系,寫出兩個面法向量再根據向量的夾角公式即可得余弦值
解析:(1)證明:∵四邊形![]() 為菱形,
為菱形, ![]() ,
,
∴![]() 為正三角形.又
為正三角形.又![]() 為
為![]() 的中點,∴
的中點,∴![]() .
.
又![]() ,因此
,因此![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,∴
,∴![]() .
.

(2)如圖, ![]() 為
為![]() 上任意一點,連接
上任意一點,連接![]() ,
, ![]() .
.

當線段![]() 長的最小時,
長的最小時, ![]() ,由(1)知
,由(1)知![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .
.
由(1)知![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,建立如圖所示的空間直角坐標系,又
為坐標原點,建立如圖所示的空間直角坐標系,又![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,
的中點,
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 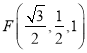 ,
,
所以![]() ,
,  .
.
設平面![]() 的一法向量為
的一法向量為![]() ,
,
則![]() 因此
因此 ,
,
取![]() ,則
,則![]() ,
,
因為![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 為平面
為平面![]() 的一法向量.又
的一法向量.又![]() ,
,
所以![]()

![]() .
.
易得二面角![]() 為銳角,故所求二面角的余弦值為
為銳角,故所求二面角的余弦值為![]() .
.

【題型】解答題
【結束】
20
【題目】【2018湖北七市(州)教研協作體3月高三聯考】已知橢圓![]() :
: ![]()
![]() 的左頂點為
的左頂點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 與直線
與直線![]() 垂直,垂足為
垂直,垂足為![]() 點,且點
點,且點![]() 是線段
是線段![]() 的中點.
的中點.

(I)求橢圓![]() 的方程;
的方程;
(II)如圖,若直線![]() :
: ![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,且四邊形
上,且四邊形![]() 為平行四邊形,求證:四邊形
為平行四邊形,求證:四邊形![]() 的面積
的面積![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市場份額又稱市場占有率,它在很大程度上反映了企業的競爭地位和盈利能力,是企業非常重視的一個指標.近年來,服務機器人與工業機器人以迅猛的增速占領了中國機器人領域龐大的市場份額,隨著“一帶一路”的積極推動,包括機器人產業在內的眾多行業得到了更廣闊的的發展空間,某市場研究人員為了了解某機器人制造企業的經營狀況,對該機器人制造企業2017年1月至6月的市場份額進行了調查,得到如下資料:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
市場份額 | 11 | 163 | 16 | 15 | 20 | 21 |
請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程,并預測該企業2017年7月份的市場份額.
的線性回歸方程,并預測該企業2017年7月份的市場份額.
如圖是該機器人制造企業記錄的2017年6月1日至6月30日之間的產品銷售頻數(單位:天)統計圖.設銷售產品數量為![]() ,經統計,當
,經統計,當![]() 時,企業每天虧損約為200萬元;
時,企業每天虧損約為200萬元;
當![]() 時,企業平均每天收入約為400萬元;
時,企業平均每天收入約為400萬元;
當![]() 時,企業平均每天收入約為700萬元.
時,企業平均每天收入約為700萬元.
①設該企業在六月份每天收入為![]() ,求
,求![]() 的數學期望;
的數學期望;
②如果將頻率視為概率,求該企業在未來連續三天總收入不低于1200萬元的概率.
附:回歸直線的方程是![]() ,其中
,其中
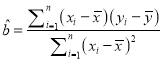 ,
, ![]() ,
,
![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在固定壓力差(壓力差為常數)下,當氣體通過圓形管道時,其流量速率,(單位:![]() )與管道半徑r(單位:cm)的四次方成正比.
)與管道半徑r(單位:cm)的四次方成正比.
(1)寫出氣體流量速率,關于管道半徑r的函數解析式;
(2)若氣體在半徑為3cm的管道中,流量速率為![]() ,求該氣體通過半徑為r的管道時,其流量速率v的表達式;
,求該氣體通過半徑為r的管道時,其流量速率v的表達式;
(3)已知(2)中的氣體通過的管道半徑為5cm,計算該氣體的流量速率(精確到![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點P是直線
,點P是直線![]() 上的一動點,過點P作圓M的切線PA,PB,切點為A,B.
上的一動點,過點P作圓M的切線PA,PB,切點為A,B.
(1)當切線PA的長度為![]() 時,求點P的坐標;
時,求點P的坐標;
(2)若![]() 的外接圓為圓N,試問:當P運動時,圓N是否過定點?若存在,求出所有的定點的坐標;若不存在,請說明理由;
的外接圓為圓N,試問:當P運動時,圓N是否過定點?若存在,求出所有的定點的坐標;若不存在,請說明理由;
(3)求線段AB長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據某鎮家庭抽樣調查的統計,2003年每戶家庭平均消費支出總額為1萬元,其中食品消費額為0.6萬元.預測2003年后,每戶家庭平均消費支出總額每年增加3000元,如果到2005年該鎮居民生活狀況能達到小康水平(即恩格爾系數n滿足![]() ),則這個鎮每戶食品消費額平均每年的增長率至多是多少(精確到0.1%)?
),則這個鎮每戶食品消費額平均每年的增長率至多是多少(精確到0.1%)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com