
【題目】設定義域為(0,+∞)的單調函數f(x),對任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一個解,且x0∈(a,a+1)(a∈N*),則實數a=
【答案】1
【解析】解:根據題意,對任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,又由f(x)是定義在(0,+∞)上的單調函數,
則f(x)﹣log2x為定值,
設t=f(x)﹣log2x,則f(x)=t+log2x,
又由f(t)=6,可得t+log2t=6,
可解得t=4,故f(x)=4+log2x,f′(x)= ![]() ,
,
又x0是方程f(x)﹣f′(x)=4的一個解,
所以x0是函數F(x)=f(x)﹣f′(x)﹣4=log2x﹣ ![]() 的零點,
的零點,
分析易得F(1)=﹣ ![]() <0,F(2)=1﹣
<0,F(2)=1﹣ ![]() =1﹣
=1﹣ ![]() >0,
>0,
故函數F(x)的零點介于(1,2)之間,故a=1,
所以答案是:1
【考點精析】通過靈活運用基本求導法則,掌握若兩個函數可導,則它們和、差、積、商必可導;若兩個函數均不可導,則它們的和、差、積、商不一定不可導即可以解答此題.


科目:高中數學 來源: 題型:
【題目】某商場計劃銷售某種產品,現邀請生產該產品的甲、乙兩個廠家進場試銷![]() 天,兩個廠家提供的返利,方案如下:甲廠家每天固定返利
天,兩個廠家提供的返利,方案如下:甲廠家每天固定返利![]() 元,且每賣出一件產品廠家再返利
元,且每賣出一件產品廠家再返利![]() 元,乙廠家無固定返利,賣出
元,乙廠家無固定返利,賣出![]() 件以內(含
件以內(含![]() 件)的產品,每件產品廠家返利
件)的產品,每件產品廠家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分別記錄其
元,分別記錄其![]() 天內的銷售件數,得到如下頻數表:
天內的銷售件數,得到如下頻數表:
甲廠家銷售件數頻數表:
銷售件數 |
|
|
|
|
|
天數 |
|
|
|
|
|
乙廠家銷售件數頻數表:
銷售件數 |
|
|
|
|
|
天數 |
|
|
|
|
|
(1) 現從甲廠家試銷的![]() 天中抽取兩天,求一天銷售量大于
天中抽取兩天,求一天銷售量大于![]() 而另一天銷售量小于
而另一天銷售量小于![]() 的概率;
的概率;
(2)若將頻率視作概率,回答以下問題:
①記乙廠家的日返利為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望;
的分布列和數學期望;
②商場擬在甲、乙兩個廠家中選擇一家長期銷售,如果僅從日返利額的角度考慮,請利用所學的統計學知識為商場作出選擇,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知單調遞增的等比數列{an}滿足a2+a3+a4=28,且a3+2是a2 , a4的等差中項. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn=anlog2an , 其前n項和為Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)對于n≥2恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,若sin(A+B﹣C)=sin(A﹣B+C),則△ABC必是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,O為坐標原點,點F為拋物線C1: ![]() 的焦點,且拋物線C1上點M處的切線與圓C2:
的焦點,且拋物線C1上點M處的切線與圓C2: ![]() 相切于點Q.
相切于點Q.
![]()
![]()
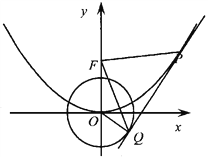
(Ⅰ)當直線MQ的方程為![]() 時,求拋物線C1的方程;
時,求拋物線C1的方程;
(Ⅱ)當正數p變化時,記S1 ,S2分別為△FMQ,△FOQ的面積,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n∈N,f(x)=(1+x)m+(1+x)n .
(1)當m=n=5時,若 ![]() ,求a0+a2+a4的值;
,求a0+a2+a4的值;
(2)f(x)展開式中x的系數是9,當m,n變化時,求x2系數的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=cos(x+φ)的圖象上每點的橫坐標縮短為原來的 ![]() 倍(縱坐標不變),再將所得的圖象向左平移
倍(縱坐標不變),再將所得的圖象向左平移 ![]() 個單位長度后得到的圖象關于坐標原點對稱,則下列直線中是函數f(x)圖象的對稱軸的是( )
個單位長度后得到的圖象關于坐標原點對稱,則下列直線中是函數f(x)圖象的對稱軸的是( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+bx+c(b,c∈R),并設 ![]() ,
,
(1)若F(x)圖像在x=0處的切線方程為x﹣y=0,求b、c的值;
(2)若函數F(x)是(﹣∞,+∞)上單調遞減,則 ①當x≥0時,試判斷f(x)與(x+c)2的大小關系,并證明之;
②對滿足題設條件的任意b、c,不等式f(c)﹣Mc2≤f(b)﹣Mb2恒成立,求M的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com