【題目】（1）用籬笆圍一個面積為
的矩形菜園，當這個矩形的邊長為多少時，所用籬笆最短？最短籬笆的長度是多少？
（2）用一段長為
的籬笆圍成一個矩形菜園，當這個矩形的邊長為多少時，菜園的面積最大？最大面積是多少？
【答案】（1）當這個矩形菜園是邊長為
的正方形時，最短籬笆的長度為
；（2）當這個矩形菜園是邊長為
的正方形時，最大面積是
.
【解析】
設矩形菜園的相鄰兩條邊的長分別為
、
，籬笆的長度為
.
（1）由題意得出
，利用基本不等式可求出矩形周長的最小值，由等號成立的條件可得出矩形的邊長，從而可得出結論；
（2）由題意得出
，利用基本不等式可求出矩形面積的最大值，由等號成立的條件可得出矩形的邊長，從而可得出結論.
設矩形菜園的相鄰兩條邊的長分別為、，籬笆的長度為.
（1）由已知得，由
，可得
，所以
，
當且僅當
時，上式等號成立.
因此，當這個矩形菜園是邊長為的正方形時，所用籬笆最短，最短籬笆的長度為；
（2）由已知得
，則，矩形菜園的面積為
.
由
，可得
，
當且僅當
時，上式等號成立.
因此，當這個矩形菜園是邊長為的正方形時，菜園的面積最大，最大面積是.
中考解讀考點精練系列答案科目：高中數學 來源： 題型：
【題目】抽樣得到某次考試中高二年級某班
名學生的數學成績和物理成績如下表：
學生編號 |
|
|
|
|
|
|
數學成績 |
|
|
|
|
|
|
物里成績 |
|
|
|
|
|
|
(1)在圖中畫出表中數據的散點圖；
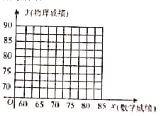
(2)建立
關于
的回歸方程：(系數保留到小數點后兩位).
(3)如果某學生的數學成績為
分，預測他本次的物理成績(成績取整數).
參考公式：回歸方程為
，其中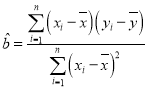
，
.
參考數據：
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為
，
為
軸上的點.
（1）當
時，過點
作直線
與
相切，求切線的方程；
（2）存在過點且傾斜角互補的兩條直線
，
，若，與分別交于
，
和
，
四點，且
與
的面積相等，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場在促銷期間規定：商場內所有商品按標價的
出售，當顧客在商場內消費一定金額后，按如下方案獲得相應金額的獎券：
消費金額（元）的范圍 |
|
|
|
| … |
獲得獎券的金額（元） | 30 | 60 | 100 | 130 | … |
根據上述促銷方法，顧客在該商場購物可以獲得雙重優惠，例如：購買標價為400元的商品，則消費金額為320元，獲得的優惠額為：
元，設購買商品得到的優惠率＝（購買商品獲得的優惠額）/（商品標價），試問：
（1）若購買一件標價為1000元的商品，顧客得到的優惠率是多少？
（2）對于標價在
（元）內的商品，顧客購買標價為多少元的商品，可得到不小于
的優惠率？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形
為正方形，四邊形
為直角梯形，且
， 
，平面
平面
， 
．
（
）求證： 
平面
．
（
）若二面角
為直二面角，
（i）求直線
與平面
所成角的大小．
（ii）棱
上是否存在點
，使得
平面
？若存在，求出
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某民營企業生產A，B兩種產品，根據市場調查與預測，A產品的利潤y與投資x成正比，其關系如圖甲，B產品的利潤y與投資x的算術平方根成正比，其關系如圖乙
注：利潤與投資單位為萬元
分別將A，B兩種產品的利潤y表示為投資x的函數關系式；
該企業已籌集到10萬元資金，并全部投入A，B兩種產品的生產
問：怎樣分配這10萬元資金，才能使企業獲得最大利潤，最大利潤是多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中：
①若函數
的定義域為
，則
一定是偶函數；
②若
是定義域上奇函數，
，都有
，則的圖像關于直線
對稱；
③已知
，
是函數
的定義域內的任意兩個值，且
，若
，則是定義域減函數；
④已知是定義在上奇函數，且
也為奇函數，則是以4為周期的周期函數。
其中真命題的有_____________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
