
【題目】某鎮在政府“精準扶貧”的政策指引下,充分利用自身資源,大力發展養殖業,以增加收入,政府計劃共投入72萬元,全部用于甲、乙兩個合作社,每個合作社至少要投入15萬元,其中甲合作社養魚,乙合作社養雞,在對市場進行調研分析發現養魚的收益M、養雞的收益N與投入a(單位:萬元)滿足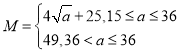 ,N=
,N=![]() a+20.設甲合作社的投入為x(單位:萬元),兩個合作社的總收益為f(x)(單位:萬元).
a+20.設甲合作社的投入為x(單位:萬元),兩個合作社的總收益為f(x)(單位:萬元).
(1)當甲合作社的投入為25萬元時,求兩個合作社的總收益;
(2)試問如何安排甲、乙兩個合作社的投入,才能使總收益最大,最大總收益為多少萬元?
【答案】(1)88.5萬元
(2)該公司在甲合作社投入16萬元,在乙合作社投入56萬元,總收益最大,最大總收益為89萬元
【解析】
根據題意,當甲合作社投入為25萬元時,乙合作社投入為47萬元,分別代入其收益與投入的函數式,最后求和即可。
首先確定函數定義域,然后結合分段函數的解析式分類討論確定最大收益的安排方法即可得出答案。
解:(1)當甲合作社投入為25萬元時,乙合作社投入為47萬元,此時兩個個合作社的總收益為:
![]() =88.5(萬元);
=88.5(萬元);
(2)甲合作社的投入為x萬元(15≤x≤57),則乙合作社的投入為72﹣x萬元,
當15≤x≤36時,則36≤72﹣x≤57,
f(x)=4![]() +25+
+25+![]() (72﹣x)+20=﹣
(72﹣x)+20=﹣![]() x+4
x+4![]() +81.
+81.
令t=![]() ,得
,得![]() ≤t≤6,
≤t≤6,
則總收益為g(t)=﹣![]() t2+4t+81=﹣
t2+4t+81=﹣![]() (t﹣4)2+89,
(t﹣4)2+89,
顯然當t=4時,函數取得最大值g(t)=89=f(16),
即此時甲投入16萬元,乙投入56萬元時,總收益最大,最大收益為89萬元
當36<x≤57時,則15<72﹣x≤36,
則f(x)=49+![]() (72﹣x)+20=﹣
(72﹣x)+20=﹣![]() x+105,
x+105,
則f(x)在(36,57]上單調遞減,
∴f(x)<f(36)=87.
即此時甲、乙總收益小于87萬元.
又89>87,
∴該公司在甲合作社投入16萬元,在乙合作社投入56萬元,總收益最大,最大總收益為89萬元.


科目:高中數學 來源: 題型:
【題目】為了了解我市參加2018年全國高中數學聯賽的學生考試結果情況,從中選取60名同學將其成績(百分制,均為正數)分成![]() 六組后,得到部分頻率分布直方圖(如圖),觀察圖形,回答下列問題:
六組后,得到部分頻率分布直方圖(如圖),觀察圖形,回答下列問題:
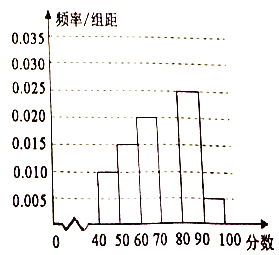
(1)求分數在![]() 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(2)根據頻率分布直方圖,估計本次考試成績的眾數、均值;
(3)根據評獎規則,排名靠前10%的同學可以獲獎,請你估計獲獎的同學至少需要所少分?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|1≤x≤3},B={x|x>2}.
(Ⅰ)分別求A∩B,(RB)∪A;
(Ⅱ)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是平行四邊形
是平行四邊形![]() 所在平面外一點,如果
所在平面外一點,如果![]() ,
,![]() ,
,![]() .(1)求證:
.(1)求證:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四邊形![]() 的面積.
的面積.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:
(1)由題意結合空間向量數量積的運算法則計算可得![]() ,
,![]() .則
.則![]() ,
,![]() ,結合線面垂直的判斷定理可得
,結合線面垂直的判斷定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐標計算可得![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
試題解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【題型】解答題
【結束】
19
【題目】(1)求圓心在直線![]() 上,且與直線
上,且與直線![]() 相切于點
相切于點![]() 的圓的方程;
的圓的方程;
(2)求與圓![]() 外切于點
外切于點![]() 且半徑為
且半徑為![]() 的圓的方程.
的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)=3x![]() .
.
(1)若f(x)=8,求x的值;
(2)對于任意的x∈[0,2],[f(x)-3]3x+13-m≥0恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界.已知函數
的上界.已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的值域,并判斷函數
上的值域,并判斷函數![]() 在
在![]() 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若![]() 是
是![]() 上的有界函數,且
上的有界函數,且![]() 的上界為3,求實數
的上界為3,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河南濮陽市高三一模】已知點![]() 在拋物線
在拋物線![]() 上,
上, ![]() 是拋物線上異于
是拋物線上異于![]() 的兩點,以
的兩點,以![]() 為直徑的圓過點
為直徑的圓過點![]() .
.
(I)證明:直線![]() 過定點;
過定點;
(II)過點![]() 作直線
作直線![]() 的垂線,求垂足
的垂線,求垂足![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com