
已知函數(shù) 的最大值為2.
的最大值為2.
(Ⅰ)求函數(shù) 在
在 上的單調(diào)遞減區(qū)間;
上的單調(diào)遞減區(qū)間;
(Ⅱ) 中,
中, ,角
,角 所對的邊分別是
所對的邊分別是 ,且
,且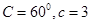 ,求
,求 的面積.
的面積.
(Ⅰ)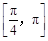 (Ⅱ)
(Ⅱ)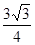
解析試題分析:(1).先由已知條件求出m值確定函數(shù)解析式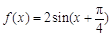 ,再由
,再由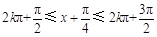
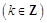 可得函數(shù)在
可得函數(shù)在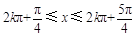
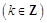 遞減區(qū)間,從而得出
遞減區(qū)間,從而得出 在
在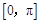 上的單調(diào)遞減區(qū)間為
上的單調(diào)遞減區(qū)間為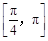 ;(Ⅱ)先由已知條件化簡得
;(Ⅱ)先由已知條件化簡得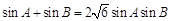 ,再由正弦定理和余弦定理得
,再由正弦定理和余弦定理得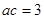 ,從而由正弦面積公式求出
,從而由正弦面積公式求出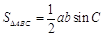
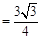 .
.
試題解析:(1)由題意, 的最大值為
的最大值為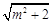 ,所以
,所以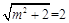 .
.
而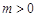 ,于是
,于是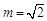 ,
,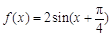 .
.  為遞減函數(shù),則
為遞減函數(shù),則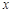 滿足
滿足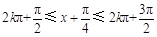
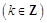 ,
,
即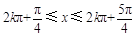
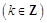 .
.
所以 在
在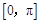 上的單調(diào)遞減區(qū)間為
上的單調(diào)遞減區(qū)間為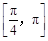 .
.
(2)設(shè)△ABC的外接圓半徑為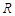 ,由題意,得
,由題意,得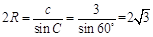 .
.
化簡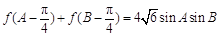 ,得
,得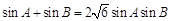 .
.
由正弦定理,得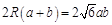 ,
,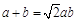 . ①
. ①
由余弦定理,得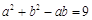 ,即
,即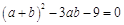 . ②
. ②
將①式代入②,得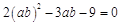 .
.
解得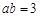 ,或
,或 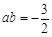 (舍去).
(舍去).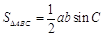
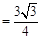 .
.
考點:1.三角函數(shù)的單調(diào)性;2.正、余弦定理;3.解三角形


科目:高中數(shù)學 來源: 題型:解答題
已知向量 ,
, ,(
,( ,且
,且 為常數(shù)),設(shè)函數(shù)
為常數(shù)),設(shè)函數(shù) ,若
,若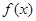 的最大值為1.
的最大值為1.
(1)求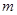 的值,并求
的值,并求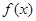 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)在 中,角
中,角 、
、 、
、 的對邊
的對邊 、
、 、
、 ,若
,若 ,且
,且 ,試判斷三角形的形狀.
,試判斷三角形的形狀.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
我艦在島A南偏西50°相距12海里的B處發(fā)現(xiàn)敵艦正從島A沿北偏西10°的方向以每小時10海里的速度航行,若我艦要用2小時追上敵艦,求我艦的速度
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com