【題目】已知函數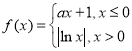
，給出下列三個結論：
①當
時，函數
的單調遞減區間為
；
②若函數無最小值，則
的取值范圍為
；
③若
且
，則
，使得函數
.恰有3個零點
，
，
，且
．
其中，所有正確結論的序號是______．
走進文言文系列答案科目：高中數學 來源： 題型：
【題目】成都七中為了解班級衛生教育系列活動的成效，對全校40個班級進行了一次突擊班級衛生量化打分檢查（滿分100分，最低分20分）.根據檢查結果：得分在
評定為“優”，獎勵3面小紅旗；得分在
評定為“良”，獎勵2面小紅旗；得分在
評定為“中”，獎勵1面小紅旗；得分在
評定為“差”，不獎勵小紅旗.已知統計結果的部分頻率分布直方圖如圖：
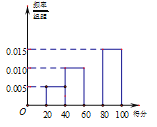
（1）依據統計結果的部分頻率分布直方圖，求班級衛生量化打分檢查得分的中位數；
（2）學校用分層抽樣的方法，從評定等級為“良”、“中”的班級中抽取6個班級，再從這6個班級中隨機抽取2個班級進行抽樣復核，求所抽取的2個班級獲得的獎勵小紅旗面數和不少于3的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】方艙醫院的啟用在本次武漢抗擊新冠疫情的關鍵時刻起到了至關重要的作用，圖1為某方艙醫院的平面設計圖，其結構可以看成矩形在四個角處對稱地截去四個全等的三角形所得，圖2中所示多邊形
，整體設計方案要求：內部井字形的兩根水平橫軸
米，兩根豎軸
米，記整個方艙醫院的外圍隔離線（圖2實線部分，軸和邊框的粗細忽略不計）總長度為
，
與
、
的交點為
、
，
與、的交點為
、
，
（
）.
（1）若
，且兩根橫軸之間的距離
米，求外圍隔離線總長度；
（2）由于疫情需要，外圍隔離線總長度不超過240米，當整個方艙醫院（多邊形的面積）最大時，給出此設計方案中
的大小與
的長度.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用
表示一個小于或等于
的最大整數.如：
，
，
. 已知實數列
、
、
對于所有非負整數
滿足
，其中是任意一個非零實數.
（Ⅰ）若
，寫出、
、
；
（Ⅱ）若
，求數列
的最小值；
（Ⅲ）證明：存在非負整數
，使得當
時，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
與
軸正半軸交于點
，與
軸交于
、
兩點.
（1）求過、、三點的圓
的方程；
（2）若
為坐標原點，直線
與橢圓
和（1）中的圓分別相切于點
和點
（、不重合），求直線
與直線
的斜率之積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某央企在一個社區隨機采訪男性和女性用戶各50名，統計他（她）們一天（
）使用手機的時間，其中每天使用手機超過6小時（含6小時）的用戶稱為“手機迷”，否則稱其為“非手機迷”，調查結果如下：
男性用戶的頻數分布表
男性用戶日用時間分組（ |
|
|
|
|
|
頻數 | 20 | 12 | 8 | 6 | 4 |
女性用戶的頻數分布表
女性用戶日用時間分組（ |
|
|
|
|
|
頻數 | 25 | 10 | 6 | 8 | 1 |
（1）分別估計男性用戶，女性用戶“手機迷”的頻率；
（2）求男性用戶每天使用手機所花時間的中位數；
（3）求女性用戶每天使用手機所花時間的平均數與標準差（同一組中的數據用該組區間的中點值作代表）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“熔噴布”是口罩生產的重要原材料，1噸熔噴布大約可供生產100萬只口罩.2020年，制造口罩的企業甲的熔噴布1月份的需求量為100噸，并且從2月份起，每月熔噴布的需求量均比上個月增加10%.企業乙是企業甲熔噴布的唯一供應商，企業乙2020年1月份的產能為100噸，為滿足市場需求，從2月份到
月份（
且
），每個月比上個月增加一條月產量為50噸的生產線投入生產，從
月份到9月份不再增加新的生產線.計劃截止到9月份，企業乙熔噴布的總產量除供應企業甲的需求外，還剩余不少于990噸的熔噴布可供給其它廠商，則企業乙至少要增加___條熔噴布生產線.
（參考數據：
，
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
