
【題目】已知函數![]() (
(![]() 為自然對數的底數,
為自然對數的底數,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表達式;
的表達式;
⑵若![]() 時,方程
時,方程![]() 在
在![]() 上恰有兩個相異實根,求實根
上恰有兩個相異實根,求實根![]() 的取值范圍;
的取值范圍;
⑶若![]() ,
,![]() ,求使
,求使![]() 得圖像恒在
得圖像恒在![]() 圖像上方的最大正整數
圖像上方的最大正整數![]() .
.
【答案】(1)
![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)借助題設條件運用分類整合思想求解;(2)依據題設運用化歸轉化的數學思想進行探求;(3)依據題設構造函數![]() ,運用導數的知識求解.
,運用導數的知識求解.
試題解析:
(1)![]() 時,
時,![]() ,
,
![]() ;
;
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為增函數,此時
上為增函數,此時![]() ,
,
②當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為增函數,
上為增函數,
故![]() 在
在![]() 上為增函數,此時
上為增函數,此時![]() …………………………………2分
…………………………………2分
③當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數,
上為減函數,
若![]() ,即/span>
,即/span>![]() 時,故
時,故![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數,
上為減函數,
此時![]() ………………………………5分
………………………………5分
若![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上為增函數,則此時
上為增函數,則此時![]() ,
,
綜上所述:
![]() ………………………………6分,
………………………………6分,
(2)![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,……………7分
上單調遞增,……………7分
![]()
![]() 在
在![]() 上恰有兩個相異實根,
上恰有兩個相異實根,
 ,
,
![]() 實數
實數![]() 的取值范圍是
的取值范圍是![]() ,…………………………………10分
,…………………………………10分
(3)由題設:![]() ,
,![]() ,(*)
,(*)
![]() ,故
,故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() (*)
(*)![]() ,
,
設![]() ,則
,則![]() ,
,
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,…………………………12分
上單調遞減,…………………………12分
而![]() ,
,
且![]() ,
,
故存在![]() ,使
,使![]() ,
,
且![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
又![]() ,
,![]() ,
,![]() 時,使
時,使![]() 的圖像恒在
的圖像恒在![]() 圖像的上方的最大整數
圖像的上方的最大整數![]() ………………14分.
………………14分.


科目:高中數學 來源: 題型:
【題目】橢圓![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,焦點到短軸端點的距離為2,離心率為
軸上,焦點到短軸端點的距離為2,離心率為![]() .
.
(Ⅰ)求該橢圓的方程;
(Ⅱ)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點且
兩點且![]() ,是否存在以原點
,是否存在以原點![]() 為圓心的定圓與直線
為圓心的定圓與直線![]() 相切?若存在求出定圓的方程;若不存在,請說明理由
相切?若存在求出定圓的方程;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e=![]() ,連結橢圓的四個頂點得到的菱形的面積為4.
,連結橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程;
(2)設直線l與橢圓相交于不同的兩點A,B.已知點A的坐標為(-a,0).若|AB|=![]() ,求直線l的傾斜角.
,求直線l的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+x2-xlna,a>1.
(1)求證:函數f(x)在(0,+∞)上單調遞增;
(2)對任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確立下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響.對近
(單位:千元)的影響.對近![]() 年的宣傳費
年的宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.
表中![]()

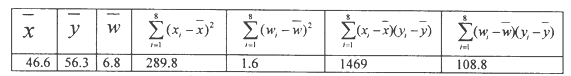
(Ⅰ)根據散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(Ⅱ)根據(Ⅰ)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ)已知這種產品的年利率![]() 與
與![]() 的關系為
的關系為![]() .根據(Ⅱ)的結果回答下列問題:
.根據(Ⅱ)的結果回答下列問題:
(i)年宣傳費![]() 時,年銷售量及利潤的預報值是多少?
時,年銷售量及利潤的預報值是多少?
(ii)年宣傳費![]() 為何值時,年利率的預報值最大?
為何值時,年利率的預報值最大?
附:對于一組數據![]() ……
……![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為:  ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
已知函數![]() (
(![]() 為常數)的圖像與
為常數)的圖像與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值及函數
的值及函數![]() 的極值;
的極值;
(2)證明:當![]() 時,
時,![]()
(3)證明:對任意給定的正數![]() ,總存在
,總存在![]() ,使得當
,使得當![]() 時,恒有
時,恒有![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用0,1,2, 3,4,5這六個數字:
(1)能組成多少個無重復數字的四位偶數?
(2)能組成多少個無重復數字且為5的倍數的五位數?
(3)能組成多少個無重復數字且比1325大的四位數?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com