
【題目】有六名同學參加演講比賽,編號分別為1,2,3,4,5,6,比賽結果設特等獎一名,![]() ,
,![]() ,
,![]() ,
,![]() 四名同學對于誰獲得特等獎進行預測.
四名同學對于誰獲得特等獎進行預測.![]() 說:不是1號就是2號獲得特等獎;
說:不是1號就是2號獲得特等獎;![]() 說:3號不可能獲得特等獎;
說:3號不可能獲得特等獎;![]() 說:4,5,6號不可能獲得特等獎;
說:4,5,6號不可能獲得特等獎;![]() 說:能獲得特等獎的是4,5,6號中的一個.公布的比賽結果表明,
說:能獲得特等獎的是4,5,6號中的一個.公布的比賽結果表明,![]() ,
,![]() ,
,![]() ,
,![]() 中只有一個判斷正確.根據(jù)以上信息,獲得特等獎的是( )號同學.
中只有一個判斷正確.根據(jù)以上信息,獲得特等獎的是( )號同學.
A.1B.2C.3D.4,5,6號中的一個
科目:高中數(shù)學 來源: 題型:
【題目】某工廠為提高生產(chǎn)效率,開展技術創(chuàng)新活動,提出了完成某項生產(chǎn)任務的兩種新的生產(chǎn)方式.為比較兩種生產(chǎn)方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產(chǎn)方式,第二組工人用第二種生產(chǎn)方式.根據(jù)工人完成生產(chǎn)任務的工作時間(單位:min)繪制了如下莖葉圖:
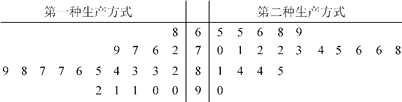
(1)根據(jù)莖葉圖判斷哪種生產(chǎn)方式的效率更高?并說明理由;
(2)求40名工人完成生產(chǎn)任務所需時間的中位數(shù)![]() ,并將完成生產(chǎn)任務所需時間超過
,并將完成生產(chǎn)任務所需時間超過![]() 和不超過
和不超過![]() 的工人數(shù)填入下面的列聯(lián)表:
的工人數(shù)填入下面的列聯(lián)表:
超過 | 不超過 | |
第一種生產(chǎn)方式 | ||
第二種生產(chǎn)方式 |
(3)根據(jù)(2)中的列聯(lián)表,能否有99%的把握認為兩種生產(chǎn)方式的效率有差異?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知圓方程為![]() ,過圓上任意一點作圓的切線,切線與橢圓
,過圓上任意一點作圓的切線,切線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 為坐標原點,設
為坐標原點,設![]() 為
為![]() 的中點,求
的中點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,曲線![]() 是由兩個定點
是由兩個定點![]() 和點
和點![]() 的距離之積等于
的距離之積等于![]() 的所有點組成的,對于曲線
的所有點組成的,對于曲線![]() ,有下列四個結論:①曲線
,有下列四個結論:①曲線![]() 是軸對稱圖形;②曲線
是軸對稱圖形;②曲線![]() 上所有的點都在單位圓
上所有的點都在單位圓![]() 內;③曲線
內;③曲線![]() 是中心對稱圖形;④曲線
是中心對稱圖形;④曲線![]() 上所有點的縱坐標
上所有點的縱坐標![]() .其中,所有正確結論的序號是______.
.其中,所有正確結論的序號是______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】
如圖,已知![]() 是以
是以![]() 的直角三角形鐵皮,
的直角三角形鐵皮,![]() 米,
米,![]() 分別是邊
分別是邊![]() 上不與端點重合的動點,且
上不與端點重合的動點,且![]() .現(xiàn)將
.現(xiàn)將![]() 鐵皮沿
鐵皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖所示.現(xiàn)要制作一個四棱錐
,如圖所示.現(xiàn)要制作一個四棱錐![]() 的封閉容器,其中
的封閉容器,其中![]() 鐵皮和直角梯形
鐵皮和直角梯形![]() 鐵皮分別是這個封閉容器的一個側面和底面,其他三個側面用相同材料的鐵皮無縫焊接密封而成(假設制作過程中不浪費材料,且鐵皮厚度忽略不計).
鐵皮分別是這個封閉容器的一個側面和底面,其他三個側面用相同材料的鐵皮無縫焊接密封而成(假設制作過程中不浪費材料,且鐵皮厚度忽略不計).
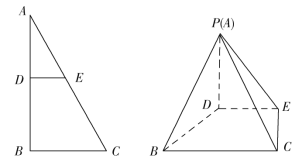
(1)若![]() 為
為![]() 邊的中點,求制作三個新增側面的鐵皮面積是多少平方米?
邊的中點,求制作三個新增側面的鐵皮面積是多少平方米?
(2)求這個封閉容器的最大體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設f(x),g(x)分別是定義在R上的奇函數(shù)和偶函數(shù),f′(x),g'(x)為其導函數(shù),當x<0時,f′(x)![]() g(x)+f(x)
g(x)+f(x)![]() g'(x)<0且g(﹣3)=0,則使得不等式f(x)
g'(x)<0且g(﹣3)=0,則使得不等式f(x)![]() g(x)<0成立的x的取值范圍是( )
g(x)<0成立的x的取值范圍是( )
A.(﹣∞,﹣3)B.(﹣3,0)C.(0,3)D.(3,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,![]() 是邊長
是邊長![]() ,
,![]() 的矩形硬紙片,在硬紙片的四角切去邊長相等的小正方形后,再沿虛線折起,做成一個無蓋的長方體盒子,
的矩形硬紙片,在硬紙片的四角切去邊長相等的小正方形后,再沿虛線折起,做成一個無蓋的長方體盒子,![]() 、
、![]() 是
是![]() 上被切去的小正方形的兩個頂點,設
上被切去的小正方形的兩個頂點,設![]() .
.

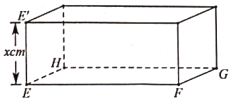
(1)將長方體盒子體積![]() 表示成
表示成![]() 的函數(shù)關系式,并求其定義域;
的函數(shù)關系式,并求其定義域;
(2)當![]() 為何值時,此長方體盒子體積
為何值時,此長方體盒子體積![]() 最大?并求出最大體積.
最大?并求出最大體積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com