
【題目】已知函數y=f(x)滿足f(x﹣1)=2x+3a,且f(a)=7.
(1)求函數f(x)的解析式;
(2)若g(x)=xf(x)+λf(x)+x在[0,2]上最大值為2,求實數λ的值.
【答案】
(1)解:f(x﹣1)=2x+3a=2(x﹣1)+3a+2,
則f(x)=2x+3a+2,
∵f(a)=7,
∴2a+3a+2=7,
解得a=1,
∴f(x)=2x+5
(2)解:g(x)=xf(x)+λf(x)+x=x(2x+5)+2λx+5λ=2x2+(6+2λ)x+5λ,
則其對稱軸為x=﹣ ![]() ,
,
當﹣ ![]() ≤0時,即λ≥﹣3時,函數g(x)在[0,2]上單調遞增,故g(x)max=g(2)=9λ+20,
≤0時,即λ≥﹣3時,函數g(x)在[0,2]上單調遞增,故g(x)max=g(2)=9λ+20,
當﹣ ![]() ≥2時,即λ≤﹣7時,函數g(x)在[0,2]上單調遞減,故g(x)max=g(0)=5λ,
≥2時,即λ≤﹣7時,函數g(x)在[0,2]上單調遞減,故g(x)max=g(0)=5λ,
當0<﹣ ![]() ≤1時,即﹣5≤λ<﹣3時,g(x)max=g(2)=9λ+20,
≤1時,即﹣5≤λ<﹣3時,g(x)max=g(2)=9λ+20,
當1<﹣ ![]() <2時,即﹣7<λ<﹣5時,g(x)max=g(0)=5λ,
<2時,即﹣7<λ<﹣5時,g(x)max=g(0)=5λ,
故,當λ≥﹣5時,g(x)max=g(2)=9λ+20=2,解得λ=﹣2,
當λ<﹣5時,g(x)max=g(0)=5λ=2,解的λ= ![]() ,舍去
,舍去
綜上所述λ的值為﹣2
【解析】(1)根據配湊法即可求出函數的解析式,(2)化簡g(x),根據二次函數的性質,分類討論即可求出λ的值,
【考點精析】利用函數的最值及其幾何意義對題目進行判斷即可得到答案,需要熟知利用二次函數的性質(配方法)求函數的最大(小)值;利用圖象求函數的最大(小)值;利用函數單調性的判斷函數的最大(小)值.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:高中數學 來源: 題型:
【題目】已知定義域為(0,+∞)的函數f(x)滿足:
①x>1時,f(x)<0;
②f( ![]() )=1;
)=1;
③對任意的正實數x,y,都有f(xy)=f(x)+f(y).
(1)求證:f( ![]() )=﹣f(x);
)=﹣f(x);
(2)求證:f(x)在定義域內為減函數;
(3)求滿足不等式f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2的m集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+bx+c滿足f(2﹣x)=f(2+x),f(0)>0,且f(m)=f(n)=0(m≠n),則log4m﹣ ![]() n的值是( )
n的值是( )
A.小于1
B.等于1
C.大于1
D.由b的符號確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣1+ ![]() ,(a∈R,e為自然對數的底數).
,(a∈R,e為自然對數的底數).
(1)求函數f(x)的單調區間;
(2)當a=1時,若直線l:y=kx﹣1與曲線y=f(x)沒有公共點,求k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科技公司生產一種手機加密芯片,其質量按測試指標劃分為:指標大于或等于![]() 為合格品,小于
為合格品,小于![]() 為次品.現隨機抽取這種芯片共
為次品.現隨機抽取這種芯片共![]() 件進行檢測,檢測結果統計如表:
件進行檢測,檢測結果統計如表:
測試指標 |
|
|
|
|
|
芯片數量(件) |
|
|
|
|
|
已知生產一件芯片,若是合格品可盈利![]() 元,若是次品則虧損
元,若是次品則虧損![]() 元.
元.
(Ⅰ)試估計生產一件芯片為合格品的概率;并求生產![]() 件芯片所獲得的利潤不少于
件芯片所獲得的利潤不少于![]() 元的概率.
元的概率.
(Ⅱ)記![]() 為生產
為生產![]() 件芯片所得的總利潤,求隨機變量
件芯片所得的總利潤,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廣播電臺為了了解某地區的聽眾對某個戲曲節目的收聽情況,隨機抽取了100名聽眾進行調查,下面是根據調查結果繪制的聽眾日均收聽該節目的頻率分布直方圖,將日均收聽該節目時間不低于40分鐘的聽眾成為“戲迷” 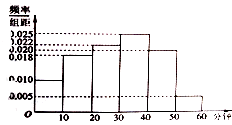
(1)根據已知條件完成2×2列聯表,并判斷“戲迷”與性別是否有關?
“戲迷” | 非戲迷 | 總計 | |
男 | |||
女 | 10 | 55 | |
總計 |
附:K2= ![]() ,
,
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
(2)將上述調查所得到的頻率當作概率.現在從該地區大量的聽眾中,采用隨機抽樣的方法每次抽取1名聽眾,抽取3次,記被抽取的3名聽眾中“戲迷”的人數為X,若每次抽取的結果相互獨立,求X的分布列,數學期望及方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系xOy中,曲線C:(x﹣1)2+y2=1.直線l經過點P(m,0),且傾斜角為 ![]() .以O為極點,以x軸正半軸為極軸,建立坐標系.
.以O為極點,以x軸正半軸為極軸,建立坐標系.
(1)寫出曲線C的極坐標方程與直線l的參數方程;
(2)若直線l與曲線C相交于A,B兩點,且|PA||PB|=1,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com