【題目】已知橢圓
過點
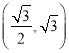，離心率為
.
（1）求橢圓的標準方程；
（2）過橢圓的上頂點作直線
交拋物線
于
兩點， 
為原點.
①求證： 
；
②設(shè)
、
分別與橢圓相交于
、
兩點，過原點
作直線
的垂線
，垂足為
，證明: 
為定值.
【答案】（1）
；（2）見解析
【解析】試題分析：（1）根據(jù)橢圓過定點以及橢圓的離心率可得
，解得
的值，由橢圓的定義可得
的值，將
的值代入橢圓方程即可得答案；（2）①設(shè)過橢圓的上頂點
的直線的
方程為
，與拋物線方程聯(lián)立，設(shè)出
點的坐標，由根與系數(shù)的關(guān)系分析計算
的值，由向量數(shù)量積的性質(zhì)可得證明；②直線
與拋物線聯(lián)立，由韋達定理及平面向量數(shù)量積公式可得， 
的等量關(guān)系，結(jié)合點到直線距離公式可得結(jié)果.
試題解析：(1) 
，所以
，又
，解得
，
，
所以橢圓的方程為
（2）①證明：設(shè)
、
，依題意，直線
一定有斜率
， 的方程為
，
聯(lián)立方程
消去
得 
，
，又
，
，
②證明：設(shè)
、
，直線
的方程為
，
，
，
，聯(lián)立方程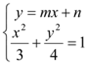
消去得 
，
，
，
而
由
得
，即
. 所以
為定值.
開心蛙狀元測試卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】選修4-4：坐標系與參數(shù)方程
在直角坐標系
中，曲線
（
為參數(shù)，
），其中
，在以
為極點，
軸正半軸為極軸的極坐標系中，曲線
，曲線
.
（Ⅰ）求
與
交點的直角坐標系；
（Ⅱ）若與
相交于點
,與相交于點
,求
的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=x2+bx+c，
（1）若函數(shù)f（x）是偶函數(shù)，求實數(shù)b的值
（2）若函數(shù)f（x）在區(qū)間[﹣1，3]上單調(diào)遞增，求實數(shù)b的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
,離心率為
,點
是橢圓上任意一點, 
的周長為
.
(Ⅰ)求橢圓
的方程；
(Ⅱ)過點
(-4,0)任作一動直線
交橢圓
于
兩點,記
,若在線段
上取一點
,使得
,則當直線
轉(zhuǎn)動時,點
在某一定直線上運動,求該定直線的方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知定義在R上的函數(shù)f（x），對任意a，b∈R，都有f（a+b）=f（a）+f（b）﹣1，當x＞0時，f（x）＞1；且f（2）=3，
（1）求f（0）及f（1）的值；
（2）判斷函數(shù)f（x）在R上的單調(diào)性，并給予證明；
（3）若f（﹣kx2）+f（kx﹣2）＜2對任意的x∈R恒成立，求實數(shù)k的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示, 
是邊長為3的正方形, 
平面
與平面
所成角為
.
(Ⅰ)求證： 
平面
；
(Ⅱ)設(shè)點
是線段
上一個動點,試確定點
的位置,使得
平面
,并證明你的結(jié)論．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）的定義域為[7，15），設(shè)f（2x+1）的定義域為A，B={x|x＜a或x＞a+1}，若A∪B=R，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=e|x|+|x|，若關(guān)于x的方程f（x）=k有兩個不同的實根，則實數(shù)k的取值范圍是 ．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
