
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() 恒成立,試確定實數
恒成立,試確定實數![]() 的取值范圍;
的取值范圍;
(3)證明![]() .
.
【答案】(1)函數![]() 的遞增區間為
的遞增區間為![]() ,函數
,函數![]() 的遞減區間為
的遞減區間為![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】試題分析:(1)先求導數![]() ,再確定導函數在定義區間上零點情況:當k≤0時,導函數恒大于零,為增函數;當k>0時,由一個零點x=
,再確定導函數在定義區間上零點情況:當k≤0時,導函數恒大于零,為增函數;當k>0時,由一個零點x=![]() ,先減后增(2)不等式恒成立問題,一般轉化Wie對應函數最值問題,即
,先減后增(2)不等式恒成立問題,一般轉化Wie對應函數最值問題,即![]() ,結合(1)的單調性情況,可得k>0且f(
,結合(1)的單調性情況,可得k>0且f(![]() )=ln
)=ln![]() ≤0解得k≥1,(3)利用導數證明不等式,一般方法為構造恰當函數,利用其增減性進行證明:因為k=1時,f(x)≤0恒成立,即ln(x﹣1)<x﹣2,令
≤0解得k≥1,(3)利用導數證明不等式,一般方法為構造恰當函數,利用其增減性進行證明:因為k=1時,f(x)≤0恒成立,即ln(x﹣1)<x﹣2,令![]() ,則
,則![]() ,代入疊加得證
,代入疊加得證
試題解析:(I)∵f(x)=ln(x﹣1)﹣k(x﹣1)+1,(x>1)
∴f′(x)=![]() ﹣k,
﹣k,
當k≤0時,f′(x)>0恒成立,故函數在(1,+∞)為增函數,
當k>0時,令f′(x)=0,得x=![]()
當f′(x)<0,即1<x<![]() 時,函數為減函數,
時,函數為減函數,
當f′(x)>0,即x>![]() 時,函數為增函數,
時,函數為增函數,
綜上所述,當k≤0時,函數f(x)在(1,+∞)為增函數,
當k>0時,函數f(x)在(1,![]() )為減函數,在(
)為減函數,在(![]() ,+∞)為增函數.
,+∞)為增函數.
(Ⅱ)由(1)知,當k≤0時,f′(x)>0函數f(x)在定義域內單調遞增,f(x)≤0不恒成立,
當k>0時,函數f(x)在(1,![]() )為減函數,在(
)為減函數,在(![]() ,+∞)為增函數.
,+∞)為增函數.
當x=![]() 時,f(x)取最大值,f(
時,f(x)取最大值,f(![]() )=ln
)=ln![]() ≤0
≤0
∴k≥1,即實數k的取值范圍為[1,+∞)
(Ⅲ)由(2)知k=1時,f(x)≤0恒成立,即ln(x﹣1)<x﹣2
∴![]() <1﹣
<1﹣![]() ,
,
∵![]() =
=![]() =
=![]() <
<![]() =
=![]()
取x=3,4,5…n,n+1累加得
∴![]() +…+
+…+![]() <
<![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ,(n∈N,n>1).
,(n∈N,n>1).


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學玩游戲,對于給定的實數a1 , 按下列方法操作一次產生一個新的實數:由甲、乙同時各擲一枚均勻的硬幣,如果出現兩個正面朝上或兩個反面朝上,則把a1乘以2后再減去12;如果出現一個正面朝上,一個反面朝上,則把a1除以2后再加上12,這樣就可以得到一個新的實數a2 , 對實數a2仍按上述方法進行一次操作,又得到一個新的實數a3 , 當a3>a1 , 甲獲勝,否則乙獲勝,若甲獲勝的概率為 ![]() ,則a1的取值范圍是( )
,則a1的取值范圍是( )
A.(﹣∞,12]
B.[24,+∞)
C.(12,24)
D.(﹣∞,12]∪[24,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .通過觀察上述兩等式的規律,請你寫出一般性的命題,并給出證明.
.通過觀察上述兩等式的規律,請你寫出一般性的命題,并給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2012年在某大學自主招生考試的面試中,七位評委為某考生打出的分數的莖葉統計圖,去掉一個最高分和一個最低分后,所剩數據的平均數和方差分別為( )
7 | 9 | ||||
8 | 4 | 4 | 6 | 4 | 7 |
9 | 3 |
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點M(x,y)在|x|≤1,|y|≤1時按均勻分布出現,試求滿足:
(1)x+y≥0的概率;
(2)x+y<1的概率;
(3)x2+y2≥1的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為選拔參加“央視猜燈謎大賽”的隊員,在校內組織猜燈謎競賽.規定:第一階段知識測試成績不小于![]() 分的學生進入第二階段比賽.現有
分的學生進入第二階段比賽.現有![]() 名學生參加知識測試,并將所有測試成績繪制成如下所示的頻率分布直方圖.
名學生參加知識測試,并將所有測試成績繪制成如下所示的頻率分布直方圖.
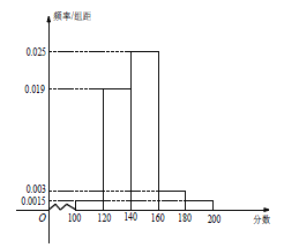
(1)估算這![]() 名學生測試成績的中位數,并求進入第二階段比賽的學生人數;
名學生測試成績的中位數,并求進入第二階段比賽的學生人數;
(2)將進入第二階段的學生分成若干隊進行比賽.現甲、乙兩隊在比賽中均已獲得![]() 分,進入最后強答階段.搶答規則:搶到的隊每次需猜
分,進入最后強答階段.搶答規則:搶到的隊每次需猜![]() 條謎語,猜對
條謎語,猜對![]() 條得
條得![]() 分,猜錯
分,猜錯![]() 條扣
條扣![]() 分.根據經驗,甲隊猜對每條謎語的概率均為
分.根據經驗,甲隊猜對每條謎語的概率均為![]() ,乙隊猜對每條謎語的概率均為
,乙隊猜對每條謎語的概率均為![]() ,猜對第
,猜對第![]() 條的概率均為
條的概率均為![]() .若這兩條搶到答題的機會均等,您做為場外觀眾想支持這兩隊中的優勝隊,會把支持票投給哪隊?
.若這兩條搶到答題的機會均等,您做為場外觀眾想支持這兩隊中的優勝隊,會把支持票投給哪隊?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F為橢圓C: ![]() +
+ ![]() =1的右焦點,橢圓C上任意一點P到點F的距離與點P到直線l:x=m的距離之比為
=1的右焦點,橢圓C上任意一點P到點F的距離與點P到直線l:x=m的距離之比為 ![]() ,求:
,求:
(1)直線l方程;
(2)設A為橢圓C的左頂點,過點F的直線交橢圓C于D、E兩點,直線AD、AE與直線l分別相交于M、N兩點.以MN為直徑的是圓是否恒過一定點,若是,求出定點坐標,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 為常數,e=2.71828…是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與x軸平行. (Ⅰ)求k的值;
為常數,e=2.71828…是自然對數的底數),曲線y=f(x)在點(1,f(1))處的切線與x軸平行. (Ⅰ)求k的值;
(Ⅱ)求f(x)的單調區間;
(Ⅲ)設g(x)=(x2+x)f′(x),其中f′(x)為f(x)的導函數.證明:對任意x>0,g(x)<1+e﹣2 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com