【題目】“雙十一”期間，某淘寶店主對其商品的上架時間
（分鐘）和銷售量
（件）的關(guān)系作了統(tǒng)計，得到如下數(shù)據(jù)：
經(jīng)計算： 
， 
， 
， 
.
（1）從滿足
的數(shù)據(jù)
中任取兩個，求所得兩個數(shù)據(jù)都滿足
的概率；
（2）該店主通過作散點圖，發(fā)現(xiàn)上架時間與銷售量線性相關(guān)，請你幫助店主求出上架時間與銷售量的線性回歸方程（保留三位小數(shù)），并預(yù)測商品上架1000分鐘時的銷售量.
【答案】(1) 
(2) 
,預(yù)測商品上架1000分鐘時銷售量約為2157件
【解析】試題分析：(1)由
得到滿足題意的6個數(shù)據(jù)，從而明確了從中任取兩個的所有結(jié)果為15，進而可得到所求的概率；（2）利用公式計算
， 
，得到回歸直線方程，即可預(yù)測商品上架1000分鐘時的銷售量.
試題解析：
（1）由表知滿足
的數(shù)據(jù)個數(shù)有6個，分別為127,133,136,138,142,147.
從中任取兩個的所有結(jié)果為：
;
;
;
;
，
共15種.其中兩個數(shù)據(jù)都滿足
的結(jié)果有6種，故所求概率
（2）由題知： 
=
=
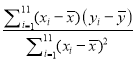=2.008
∴
=
=400-2.008125=149，∴回歸直線方程為
；
當(dāng)
時， 
，
故預(yù)測商品上架1000分鐘時銷售量約為2157件.
名師指導(dǎo)期末沖刺卷系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】通過隨機詢問110名大學(xué)生是否愛好某項運動，得到列聯(lián)表：
男 | 女 | 總計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由K2＝
，得K2＝
≈7.8.
附表：
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
參照附表，得到的正確結(jié)論是( )
A. 有99%以上的把握認為“愛好該項運動與性別有關(guān)”
B. 有99%以上的把握認為“愛好該項運動與性別無關(guān)”
C. 在犯錯誤的概率不超過0.1%的前提下，認為“愛好該項運動與性別有關(guān)”
D. 在犯錯誤的概率不超過0.1%的前提下，認為“愛好該項運動與性別無關(guān)”
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某化工廠引進一條先進生產(chǎn)線生產(chǎn)某種化工產(chǎn)品，其生產(chǎn)的總成本
（萬元）與年產(chǎn)量
（噸）之間的函數(shù)關(guān)系式可以近似的表示為
，已知此生產(chǎn)線年產(chǎn)量最大為
噸．
（1）求年產(chǎn)量為多少噸時，生產(chǎn)每噸產(chǎn)品的平均成本最低，并求最低成本；
（2）若每噸產(chǎn)品平均出廠價為40萬元，那么當(dāng)年產(chǎn)量為多少噸時，可以獲得最大利潤？最大利潤是多少？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（
為常數(shù)）與
軸有唯一的公關(guān)點
．
（Ⅰ）求函數(shù)
的單調(diào)區(qū)間；
（Ⅱ）曲線
在點
處的切線斜率為
，若存在不相等的正實數(shù)
，滿足
，證明： 
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為F1(－c，0)，F(xiàn)2(c，0)，直線
交橢圓E于A，B兩點，△ABF1的周長為16，△AF1F2的周長為12．
(1)求橢圓E的標(biāo)準(zhǔn)方程與離心率；
(2)若直線l與橢圓E交于C，D兩點，且P(2，2)是線段CD的中點，求直線l的一般方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，ABCD是邊長為3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE與平面ABCD所成角為60°．
（Ⅰ）求證：AC⊥平面BDE；
（Ⅱ）求二面角F﹣BE﹣D的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，將曲線
上的所有點橫坐標(biāo)伸長為原來的
倍，縱坐標(biāo)伸長為原來的2倍后，得到曲線
，在以
為極點， 
軸正半軸為極軸的極坐標(biāo)系中，直線
的極坐標(biāo)方程是
.
（1）寫出曲線
的參數(shù)方程和直線
的直角坐標(biāo)方程；
（2）在曲線
上求一點
，使點
到直線
的距離
最大，并求出此最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C： 
的左焦點為F(－1，0)，經(jīng)過點F的直線l0與橢圓交于A，B兩點.當(dāng)直線l0⊥x軸時，|AB|＝
.
(1)求橢圓C的方程；
(2)作直線l⊥x軸，分別過A，B作AA1⊥l，垂足為A1，BB1⊥l，垂足為B1，且△A1FB1是直角三角形.問：是否存在直線l使得∠A1FO＝2∠B1FO？若存在，求出直線l的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在數(shù)列{an}中，a1＝1，a2＝2，數(shù)列{anan＋1}是公比為q (q>0)的等比數(shù)列，則數(shù)列{an}的前2n項和S2n＝____________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com