
【題目】自然數(shù)按如圖的規(guī)律排列:則上起第2007行左起2008列的數(shù)為( ) 
A.20072
B.20082
C.2006×2007
D.2007×2008
【答案】D
【解析】解:經(jīng)觀察,這個(gè)自然數(shù)表的排列特征有:①第一列的每一個(gè)數(shù)都是完全平方數(shù),并且恰好等于它所在行數(shù)的平方,即第n行的第1個(gè)數(shù)為n2;②第一行第n個(gè)數(shù)為(n﹣1)2+1;③第n行中從第1個(gè)數(shù)至第n個(gè)數(shù)依次遞減1;④第n列中從第1個(gè)數(shù)至第n個(gè)數(shù)依次遞增1.故上起第2007行,左起第2008列的數(shù),應(yīng)是第2008列的第2007個(gè)數(shù),即為[(2008﹣1)2+1]+2006=20072+2007=2007×2008.
故選D.
【考點(diǎn)精析】通過靈活運(yùn)用等差數(shù)列的通項(xiàng)公式(及其變式),掌握通項(xiàng)公式:![]() 或
或![]() 即可以解答此題.
即可以解答此題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象與
的圖象與![]() 軸相切,且切點(diǎn)在
軸相切,且切點(diǎn)在![]() 軸的正半軸上.
軸的正半軸上.
(1)求曲線![]() 與
與![]() 軸,直線
軸,直線![]() 及
及![]() 軸圍成圖形的面積
軸圍成圖形的面積![]() ;
;
(2)若函數(shù)![]() 在
在![]() 上的極小值不大于
上的極小值不大于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐S﹣ABC中,∠ABC=90°,SA⊥平面ABC,點(diǎn)A在SB和SC上的射影分別為E、D. 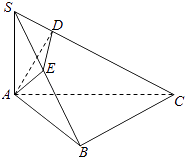
(1)求證:DE⊥SC;
(2)若SA=AB=BC=1,求直線AD與平面ABC所成角的余弦值. 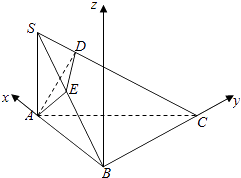
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是等差數(shù)列,滿足
是等差數(shù)列,滿足![]() ,
, ![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,
, ![]() ,且
,且![]() 是等比數(shù)列.
是等比數(shù)列.
(1)求數(shù)列![]() 和
和![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求數(shù)列![]() 的前
的前![]() 項(xiàng)和.
項(xiàng)和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】用數(shù)學(xué)歸納法證明1+2+3+…+n2= ![]() ,則當(dāng)n=k+1時(shí)左端應(yīng)在n=k的基礎(chǔ)上加上( )
,則當(dāng)n=k+1時(shí)左端應(yīng)在n=k的基礎(chǔ)上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,右頂點(diǎn)為
,右頂點(diǎn)為![]() .已知
.已知![]() ,其中
,其中![]() 為原點(diǎn),
為原點(diǎn), ![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程及離心率![]() 的值;
的值;
(2)設(shè)過點(diǎn)![]() 的直線
的直線![]() 與橢圓交于點(diǎn)
與橢圓交于點(diǎn)![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點(diǎn)
交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .若
.若![]() ,且
,且![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側(cè)面BB1C1C為菱形,B1C的中點(diǎn)為O,且AO⊥平面BB1C1C. 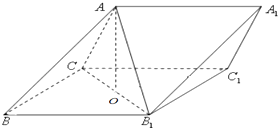
(1)證明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=2,求B1到平面ABC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中,以原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸,曲線C的極坐標(biāo)方程為ρ= ![]() . (Ⅰ)將曲線C的極坐標(biāo)方程化為直角坐標(biāo)方程;
. (Ⅰ)將曲線C的極坐標(biāo)方程化為直角坐標(biāo)方程;
(Ⅱ)過點(diǎn)P(0,2)作斜率為1直線l與曲線C交于A,B兩點(diǎn),試求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com