
【題目】已知函數![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線的方程為
處的切線的方程為![]() ,求實數
,求實數![]() 的值;
的值;
(2)設![]() ,若對任意兩個不等的正數
,若對任意兩個不等的正數![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
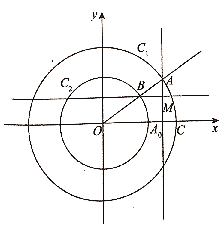
【題目】如圖所示,以原點![]() 為圓心的兩個同心圓
為圓心的兩個同心圓![]() ,其中,大圓
,其中,大圓![]() 的半徑為
的半徑為![]() ,小圓的半徑為
,小圓的半徑為![]() ,點
,點![]() 為大圓
為大圓![]() 上一動點,連接
上一動點,連接![]() ,與小圓
,與小圓![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,點
,點![]() ,記
,記![]() .
.
(1)求點![]() 的坐標(用含有
的坐標(用含有![]() 的式子表示),并寫出點
的式子表示),并寫出點![]() 的軌跡方程,指出點
的軌跡方程,指出點![]() 的軌跡是什么曲線;
的軌跡是什么曲線;
(2)設點![]() 的軌跡為
的軌跡為![]() ,點
,點![]() 分別是曲線
分別是曲線![]() 上的兩個動點,且
上的兩個動點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-5:不等式選講
已知函數f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值為2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于命題![]() :存在一個常數
:存在一個常數![]() ,使得不等式
,使得不等式![]() 對任意正數
對任意正數![]() ,
,![]() 恒成立.
恒成立.
(1)試給出這個常數![]() 的值;
的值;
(2)在(1)所得結論的條件下證明命題![]() ;
;
(3)對于上述命題,某同學正確地猜想了命題![]() :“存在一個常數
:“存在一個常數![]() ,使得不等式
,使得不等式![]() 對任意正數
對任意正數![]() ,
,![]() ,
,![]() 恒成立.”觀察命題
恒成立.”觀察命題![]() 與命題
與命題![]() 的規律,請猜想與正數
的規律,請猜想與正數![]() ,
,![]() ,
,![]() ,
,![]() 相關的命題.
相關的命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為招聘新員工設計了一個面試方案:應聘者從6道備選題中一次性隨機抽取3道題,按題目要求獨立完成.規定:至少正確完成其中2道題的便可通過.已知6道備選題中應聘者甲有4道題能正確完成,2道題不能完成;應聘者乙每題正確完成的概率都是![]() ,且每題正確完成與否互不影響.
,且每題正確完成與否互不影響.
(1)分別求甲、乙兩人正確完成面試題數的分布列及數學期望;
(2)請分析比較甲、乙兩人誰面試通過的可能性大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={(x,y)|y=f(x)},若對于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,則稱集合M是“垂直對點集”.給出下列四個集合:
①M={![]() };②M={(x,y)|y=sinx+1};
};②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};④M={(x,y)|y=ex﹣2}.
其中是“垂直對點集”的序號是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “![]() 為真”是“
為真”是“![]() 為真”的充分不必要條件;
為真”的充分不必要條件;
B. 樣本![]() 的標準差是3.3;
的標準差是3.3;
C. K2是用來判斷兩個分類變量是否相關的隨機變量,當K2的值很小時可以推定兩類變量不相關;
D. 設有一個回歸直線方程為![]() ,則變量
,則變量![]() 每增加一個單位,
每增加一個單位,![]() 平均減少1.5個單位.
平均減少1.5個單位.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某出租車公司為了解本公司出租車司機對新法規的知曉情況,隨機對![]() 名出租車司機進行調查,調查問卷共
名出租車司機進行調查,調查問卷共![]() 道題,答題情況如下表:
道題,答題情況如下表:
答對題目數 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租車司機答對題目大于等于![]() ,就認為該司機對新法規的知曉情況比較好,試估計該公司的出租車司機對新法規知曉情況比較好的概率;
,就認為該司機對新法規的知曉情況比較好,試估計該公司的出租車司機對新法規知曉情況比較好的概率;
(II)從答對題目數小于![]() 的出租車司機中選出
的出租車司機中選出![]() 人做進一步的調查,求選出的
人做進一步的調查,求選出的![]() 人中至少有一名女出租車司機的概率.
人中至少有一名女出租車司機的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com