
【題目】定義在R上的單調增函數f(x),對任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)判斷函數f(x)的奇偶性;
(2)若f(k3x)+f(3x﹣9x﹣2)<0對任意x∈R恒成立,求實數k的取值范圍.
【答案】
(1)解:令x=y=0,代入f(x+y)=f(x)+f(y)(x,y∈R),得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=﹣x,代入f(x+y)=f(x)+f(y)(x,y∈R),得 f(x﹣x)=f(x)+f(﹣x),
又f(0)=0,則有0=f(x)+f(﹣x).
即f(﹣x)=﹣f(x)對任意x∈R成立,所以f(x)是奇函數
(2)解:f(x)在R上是單調增函數,又由(1)知f(x)是奇函數.
∵f(k3x)<﹣f(3x﹣9x﹣2)=f(﹣3x+9x+2),
∴k3x<﹣3x+9x+2,
∴32x﹣(1+k)3x+2>0對任意x∈R成立.
令t=3x>0,問題等價于t2﹣(1+k)t+2>0對任意t>0恒成立.
令g(t)=t2﹣(1+k)t+2,其對稱軸為 ![]()
當 ![]() ,即k<﹣1時,g(0)>2,符合題意;
,即k<﹣1時,g(0)>2,符合題意;
當 ![]() ,即k≥﹣1時,則△=(1+k)2﹣4×2<0,∴
,即k≥﹣1時,則△=(1+k)2﹣4×2<0,∴ ![]()
綜上, ![]()
【解析】(1)根據f(x+y)=f(x)+f(y)(x,y∈R),分別令x=y=0,y=﹣x,即可證得結論;(2)根據f(x)在R上是單調增函數,且是奇函數,將f(k3x)+f(3x﹣9x﹣2)<0對任意x∈R恒成立,轉化為32x﹣(1+k)3x+2>0對任意x∈R成立,進而可利用換元法及分類討論的思想,即可求得實數k的取值范圍.
【考點精析】利用函數單調性的性質和奇偶性與單調性的綜合對題目進行判斷即可得到答案,需要熟知函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集;奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性.


科目:高中數學 來源: 題型:
【題目】某校對高二年級選學生物的學生的某次測試成績進行了統計,隨機抽取了![]() 名學生的成績作為樣本,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:
名學生的成績作為樣本,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:
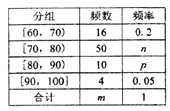

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值;
的值;
(2)如果用分層抽樣的方法,從樣本成績在![]() 和
和![]() 的學生中共抽取
的學生中共抽取![]() 人,再從
人,再從![]() 人中選
人中選![]() 人,
人,
求這![]() 人成績在
人成績在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】奇函數f(x)、偶函數g(x)的圖象分別如圖1、2所示,方程f(g(x))=0、g(f(x))=0的實根個數分別為a、b,則a+b=( ) 
A.14
B.10
C.7
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解消費者購物情況,某購物中心在電腦小票中隨機抽取![]() 張進行統計,將結果分成6組,分別是:
張進行統計,將結果分成6組,分別是: ![]() ,
, ![]() ,制成如下所示的頻率分布直方圖(假設消費金額均在
,制成如下所示的頻率分布直方圖(假設消費金額均在![]() 元的區間內).
元的區間內).
(1)若在消費金額為![]() 元區間內按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票來自
元區間內按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票來自![]() 元和
元和![]() 元區間(兩區間都有)的概率;
元區間(兩區間都有)的概率;
(2)為做好春節期間的商場促銷活動,商場設計了兩種不同的促銷方案.

方案一:全場商品打八五折.
方案二:全場購物滿100元減20元,滿300元減80元,滿500元減120元,以上減免只取最高優惠,不重復減免.利用直方圖的信息分析:哪種方案優惠力度更大,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①將一組數據中的每個數據都加上或減去同一個常數后,方差恒不變;
②設有一個回歸方程![]() ,變量
,變量![]() 增加一個單位時,
增加一個單位時, ![]() 平均增加
平均增加![]() 個單位;
個單位;
③老師在某班學號為1~50的50名學生中依次抽取學號為5,10,15,20,25,30,35,40,45,50的學生進行作業檢查,這種抽樣方法是系統抽樣;
其中正確的個數是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 0
D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com