
【題目】對于函數![]() ,若存在
,若存在![]() 成立,則稱
成立,則稱![]() 的不動點.如果函數
的不動點.如果函數
![]() 有且只有兩個不動點0,2,且
有且只有兩個不動點0,2,且![]()
(1)求函數![]() 的解析式;
的解析式;
(2)已知各項不為零的數列![]() ,求數列通項
,求數列通項![]() ;
;
(3)如果數列![]() 滿足
滿足![]() ,求證:當
,求證:當![]() 時,恒有
時,恒有![]() 成立.
成立.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】
(1)根據題意得方程![]() 有兩解0,2,代入可得
有兩解0,2,代入可得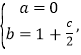 再根據
再根據![]() 得
得![]() 結合
結合![]() 解得c,b,最后代入驗證舍去不滿足題意的解,(2)代入化簡得
解得c,b,最后代入驗證舍去不滿足題意的解,(2)代入化簡得![]() 再根據和項與通項關系解得
再根據和項與通項關系解得![]() 最后代入驗證
最后代入驗證![]() ,根據等差數列通項公式求結果,(3)利用反證法,假設
,根據等差數列通項公式求結果,(3)利用反證法,假設![]() 先由
先由![]() 得
得![]() ,再根據
,再根據![]() 得
得![]() 兩者矛盾,即得結論.
兩者矛盾,即得結論.
解:設![]() 得:
得:![]() 由違達定理得:
由違達定理得: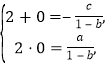
解得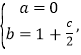 代入表達式
代入表達式![]() ,由
,由![]()
得![]() 不止有兩個不動點,
不止有兩個不動點,
![]()
(2)由題設得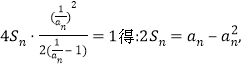 (A)
(A)
且![]() (B)
(B)
由(A)![]() (B)得:
(B)得:![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ;由
;由![]() ,若
,若![]() 這與
這與![]() 矛盾,
矛盾,
![]() ,即{
,即{![]() 是以
是以![]() 1為首項,
1為首項,![]() 1為公差的等差數列,
1為公差的等差數列,
![]() ;
;
(3)證法(一):運用反證法,假設![]() 則由(1)知
則由(1)知![]()
![]()
∴![]() ,而當
,而當![]()
這與假設矛盾,故假設不成立,∴![]() .
.
證法(二):由![]()
得![]() <0或
<0或![]() 結論成立;
結論成立;
若![]()
![]() ,此時
,此時![]() 從而
從而![]()
即數列{![]() }在
}在![]() 時單調遞減,由
時單調遞減,由![]() ,可知
,可知![]() 上成立.
上成立.


科目:高中數學 來源: 題型:
【題目】某某大學藝術專業400名學生參加某次測評,根據男女學生人數比例,使用分層抽樣的方法從中隨機抽取了100名學生,記錄他們的分數,將數據分成7組: ![]() ,并整理得到如下頻率分布直方圖:
,并整理得到如下頻率分布直方圖:

(Ⅰ)從總體的400名學生中隨機抽取一人,估計其分數小于70的概率;
(Ⅱ)已知樣本中分數小于40的學生有5人,試估計總體中分數在區間[40,50)內的人數;
(Ⅲ)已知樣本中有一半男生的分數不小于70,且樣本中分數不小于70的男女生人數相等.試估計總體中男生和女生人數的比例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,平面五邊形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是邊長為2的正三角形.現將△ADE沿AD折起,得到四棱錐E﹣ABCD(如圖2),且DE⊥AB.
(Ⅰ)求證:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成銳二面角的大小;
(Ⅲ)在棱AE上是否存在點F,使得DF∥平面BCE?若存在,求 ![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.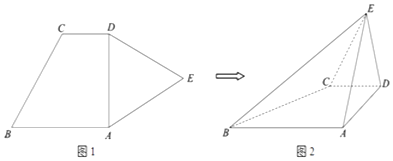
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品按質量分10個檔次,生產最低檔次的利潤是8元/件;每提高一個檔次,利潤每件增加2元,每提高一個檔次,產量減少3件,在相同時間內,最低檔次的產品可生產60件.問:在相同時間內,生產第幾檔次的產品可獲得最大利潤?(最低檔次為第一檔次)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發芽多少之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每100顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,記發芽的種子數分別為![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由線性回歸方程得到的估計數據與4月份所選5天的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的. 請根據4月7日,4月15日與4月21日這三天的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判定所得的線性回歸方程是否可靠?
,并判定所得的線性回歸方程是否可靠?
參考公式:  ,
, ![]()
參考數據: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1中,E、F分別為棱DD1和BC中點G為棱A1B1上任意一點,則直線AE與直線FG所成的角為( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C是△ABC的三個內角,則在下列各結論中,不正確的為( )
A. sin2A=sin2B+sin2C+2sinBsinCcos(B+C)
B. sin2B=sin2A+sin2C+2sinAsinCcos(A+C)
C. sin2C=sin2A+sin2B-2sinAsinBcosC
D. sin2(A+B)=sin2A+sin2B-2sinBsinCcos(A+B)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com