
【題目】已知函數![]() .
.
(I)若函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() 的值;
的值;
(II)若在區間![]() 上,函數
上,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 下方,求
下方,求![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
試題分析:(I)求導再由![]()
![]()
![]()
![]()
![]()
![]() 切線方程得:
切線方程得:![]()
![]()
![]() ;(II)令
;(II)令![]() ,再利用轉化思想將原命題等價轉化為
,再利用轉化思想將原命題等價轉化為![]() 在區間
在區間![]() 上恒成立.然后利用分類討論思想,并借助導數工具,求得:當
上恒成立.然后利用分類討論思想,并借助導數工具,求得:當![]() 時,函數
時,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 下方.
下方.
試題解析:(I)由題知,![]() ,………………1分
,………………1分
又![]() ,即
,即![]() ,∴
,∴![]() .………………2分
.………………2分
∴![]() ,∴
,∴![]() .
.
所以切點為![]() ,代入切線方程得:
,代入切線方程得:![]() ,∴
,∴![]() .………………4分
.………………4分
(II)令![]() ,則
,則![]() 的定義域為
的定義域為![]() .
.
在區間![]() 上函數
上函數![]() 的圖象恒在直線
的圖象恒在直線![]() 下方等價于
下方等價于![]() 在區間
在區間![]() 上恒成立.
上恒成立.
∵![]() ,………………5分
,………………5分
令![]() ,得
,得![]() 或
或![]() .………………6分
.………………6分
①若![]() ,則
,則![]() .∴在
.∴在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() .
.
∴![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
∴![]() ,
,
∴與![]() 在區間
在區間![]() 上恒成立相背,不符合題意.………………8分
上恒成立相背,不符合題意.………………8分
②若![]() 時,則
時,則![]() ,∵在
,∵在![]() 上有
上有![]() ,∴
,∴![]() 在區間
在區間![]() 遞增.
遞增.
∴![]() ,∴不符合題意.………………10分
,∴不符合題意.………………10分
③若![]() ,則
,則![]() ,∵在區間
,∵在區間![]() 上有
上有![]() ,則
,則![]() 在區間
在區間![]() 遞減.
遞減.
∴![]() 在
在![]() 恒成立,要使
恒成立,要使![]() 在
在![]() 恒成立,只需
恒成立,只需![]() .
.
∴![]() ,
,
∴![]() .
.
綜上,當![]() 時,函數
時,函數![]() 的圖象恒在直線
的圖象恒在直線![]() 下方.………………12分
下方.………………12分


 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,某生態園將一三角形地塊![]() 的一角
的一角![]() 開辟為水果園種植桃樹,已知角
開辟為水果園種植桃樹,已知角![]() 為
為![]() ,
,![]() 的長度均大于
的長度均大于![]() 米,現在邊界
米,現在邊界![]() 處建圍墻,在
處建圍墻,在![]() 處圍竹籬笆.
處圍竹籬笆.
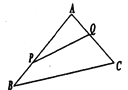
(1)若圍墻![]() 總 長度為
總 長度為![]() 米,如何圍可使得三角形地塊
米,如何圍可使得三角形地塊![]() 的面積最大?
的面積最大?
(2)已知![]() 段圍墻高
段圍墻高![]() 米,
米,![]() 段圍墻高
段圍墻高![]() 米,造價均為每平方米
米,造價均為每平方米![]() 元.若圍圍墻用了
元.若圍圍墻用了![]() 元,問如何圍可使竹籬笆用料最省?
元,問如何圍可使竹籬笆用料最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 在一個特定時段內,以點E為中心的7海里以內海域被設為警戒水域.點E正北55海里處有一個雷達觀測站A.某時刻測得一艘勻速直線行駛的船只位于點A北偏東![]() 且與點A相距40
且與點A相距40![]() 海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東
海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東![]() +
+![]() (其中sin
(其中sin![]() =
=![]() ,
,![]() )且與點A相距10
)且與點A相距10![]() 海里的位置C.
海里的位置C.
(I)求該船的行駛速度(單位:海里/小時);
(II)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司2016年前三個月的利潤(單位:百萬元)如下:
月份 |
|
|
|
利潤 |
|
|
|
(1)求利潤![]() 關于月份
關于月份![]() 的線性回歸方程;
的線性回歸方程;
(2)試用(1)中求得的回歸方程預測![]() 月和
月和![]() 月的利潤;
月的利潤;
(3)試用(1)中求得的回歸方程預測該公司2016年從幾月份開始利潤超過![]() 萬?
萬?
相關公式: 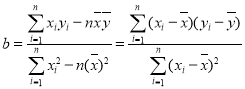 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 為原點的直角坐標系中,點
為原點的直角坐標系中,點![]() 為
為![]() 的直角頂點,已知
的直角頂點,已知![]() ,且點
,且點![]() 的縱坐標大于0.
的縱坐標大于0.
(1)求![]() 的坐標;
的坐標;
(2)求圓![]() 關于直線
關于直線![]() 對稱的圓
對稱的圓![]() 的方程;在直線
的方程;在直線![]() 上是否存在點
上是否存在點![]() ,過點
,過點![]() 的任意一條直線如果和圓
的任意一條直線如果和圓![]() 圓
圓![]() 都相交,則該直線被兩圓截得的線段長相等,如果存在求出點
都相交,則該直線被兩圓截得的線段長相等,如果存在求出點![]() 的坐標,如果不存在,請說明理由.
的坐標,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
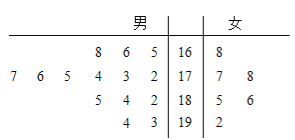
【題目】![]() 公司從某大學招收畢業生,經過綜合測試,錄用了14名男生和6名女生,這20名畢業生的測試成績如莖葉圖所示(單位:分),公司規定:成績在180分以上者到“甲部門”工作;180分以下者到“乙部門”工作.
公司從某大學招收畢業生,經過綜合測試,錄用了14名男生和6名女生,這20名畢業生的測試成績如莖葉圖所示(單位:分),公司規定:成績在180分以上者到“甲部門”工作;180分以下者到“乙部門”工作.
(1)求男生成績的中位數及女生成績的平均值;
(2)如果用分層抽樣的方法從“甲部門”人選和“乙部門”人選中共選取5人,再從這5人中選2人,那么至少有一人是“甲部門”人選的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com