
���}Ŀ����֪�E�A![]() �Ķ��S�L��2���x���ʞ�
�Ķ��S�L��2���x���ʞ�![]() ��
��![]() ��
��![]() �քe�ǙE�A������c(di��n)������c(di��n).
�քe�ǙE�A������c(di��n)������c(di��n).
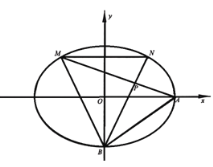
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����֪![]() �ǙE�A
�ǙE�A![]() ��(n��i)һ�c(di��n)��ֱ��
��(n��i)һ�c(di��n)��ֱ��![]() �c
�c![]() ��б��֮�e��
��б��֮�e��![]() ��ֱ��
��ֱ��![]() �քe���E�A��
�քe���E�A��![]() ���c(di��n)��ӛ
���c(di��n)��ӛ![]() ��
��![]() ����e�քe��
����e�քe��![]() ��
��![]() .
.
����![]() ���c(di��n)�P(gu��n)��
���c(di��n)�P(gu��n)��![]() �S���Q����ֱ��
�S���Q����ֱ��![]() ��б�ʣ�
��б�ʣ�
���C����![]() .
.
���𰸡���1��![]() ����2����
����2����![]() ����ԔҊ����.
����ԔҊ����.
��������
��1������(j��)���S�L��![]() ���ٸ���(j��)�x����
���ٸ���(j��)�x����![]() �Լ�
�Լ�![]() ���P(gu��n)ϵʽ�ɽ��
���P(gu��n)ϵʽ�ɽ��![]() ���Ķ�����ÙE�A
���Ķ�����ÙE�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2�����O(sh��)��![]() ���
���![]() ������
������![]() �ķ����c�E�A(li��n)�����
�ķ����c�E�A(li��n)�����![]() ������(bi��o)���ٸ���(j��)
������(bi��o)���ٸ���(j��)![]() ��б���P(gu��n)ϵ��
��б���P(gu��n)ϵ��![]() ��б�ʺͷ����c�E�A(li��n)�����
��б�ʺͷ����c�E�A(li��n)�����![]() ������(bi��o)������(j��)
������(bi��o)������(j��)![]() ��
��![]() �P(gu��n)��
�P(gu��n)��![]() �S���Q����ʽ�����
�S���Q����ʽ�����![]() ��
��
����![]() �ķ���(li��n)�����
�ķ���(li��n)�����![]() ������(bi��o)��ͨ�^���c(di��n)�g�ľ��x���
������(bi��o)��ͨ�^���c(di��n)�g�ľ��x���![]() ��ֻҪ�C��
��ֻҪ�C��![]() ���Ϳ��C��
���Ϳ��C��![]() .
.
��1���E�A![]() �Ķ��S�L��
�Ķ��S�L��![]() ���x���ʞ�
���x���ʞ�![]() ��
��
����![]() ��
��![]() ��
��
���![]() .
.
���ԙE�A���̞�![]() .
.
��2��
���O(sh��)ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ���tֱ��
���tֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
(li��n)��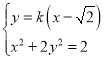 ����ȥ
����ȥ![]() ��������
��������![]() ��
��
���![]() ������
������ .
.
��?y��n)�ֱ��![]() ��б�ʳ˷e��
��б�ʳ˷e��![]() ������ֱ��
������ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
(li��n)��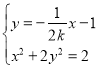 ����ȥ
����ȥ![]() ��������
��������![]() ��
��
���![]() ������
������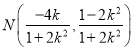 .
.
��?y��n)?/span>![]() �P(gu��n)��
�P(gu��n)��![]() �S���Q������
�S���Q������![]() ��
��
��![]() �����
�����![]() .
.
��(d��ng)![]() �r����
�r����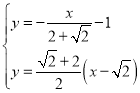 �����
�����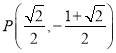 ���ڙE�A
���ڙE�A![]() �⣬���M���}��.
�⣬���M���}��.
����ֱ��![]() ��б�ʞ�
��б�ʞ�![]() .
.
���ɢٵ� ��
��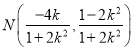 ��
��![]() ��
��
��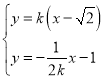 �����
�����![]() .
.
��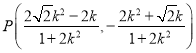 .
.
����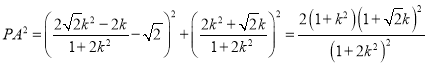 ��
��
 ��
��
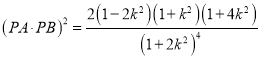 .
.
ͬ�����Ã��c(di��n)�g�ľ��x��ʽ���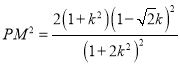 ��
��
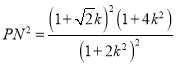 ��
��
����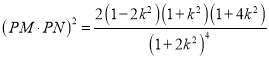 .
.
����![]() ��
��
��?y��n)?/span>![]() ������
������
![]() .
.
��![]() .
.


 ��ĩ100���J�P(gu��n)��������ϵ�д�
��ĩ100���J�P(gu��n)��������ϵ�д� С�W(xu��)�����yԇ��ϵ�д�
С�W(xu��)�����yԇ��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��![]() ����
����![]() ����
����![]() ����
����![]() �����҈D��ʾ�ij����D�У����ݔ��
�����҈D��ʾ�ij����D�У����ݔ��![]() ����ݔ��
����ݔ��![]() ���t�ڿհ�̎�����루 ��
���t�ڿհ�̎�����루 ��
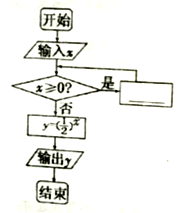
A���٢ڢ� B���ڢ� C���ۢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�W(xu��)У�߶��꼉�e������ȫ�w�W(xu��)�����ӵ�һ������K��ِ��Ӌ(j��)��Ҏ(gu��)�t���±���
ÿ������K����(sh��) |
|
|
|
|
|
�÷� | 16 | 17 | 18 | 19 | 20 |
�꼉�M���˽�W(xu��)�����w�|(zh��)���S�C(j��)��ȡ��100���W(xu��)�������K����(sh��)����һ���ӱ����L�������ӱ��l�ʷֲ�ֱ���D.
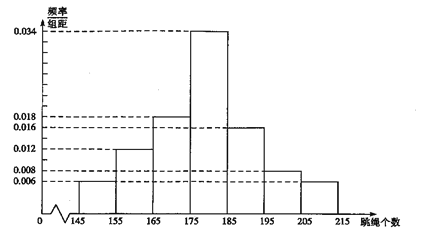
��1���F(xi��n)�Ęӱ���100���W(xu��)�����K����(sh��)�У������ȡ2�˵����K����(sh��)������˵÷�֮��С��35�ֵĸ��ʣ��������?j��n)?sh��)��ʾ��
��2����ԓУ�߶��꼉����2000���W(xu��)�������ЌW(xu��)����һ������K����(sh��)![]() ���Ʒ������B(t��i)�ֲ�
���Ʒ������B(t��i)�ֲ�![]() ������
������![]() ��
��![]() ��ӱ�ƽ����(sh��)�Ĺ�Ӌ(j��)ֵ��ͬһ�M�Д�(sh��)��(j��)���@�M��(sh��)��(j��)���څ^(q��)�g���c(di��n)ֵ��������.�������õ����B(t��i)�ֲ�ģ�ͣ���Q�����}��
��ӱ�ƽ����(sh��)�Ĺ�Ӌ(j��)ֵ��ͬһ�M�Д�(sh��)��(j��)���@�M��(sh��)��(j��)���څ^(q��)�g���c(di��n)ֵ��������.�������õ����B(t��i)�ֲ�ģ�ͣ���Q�����}��
��i����Ӌ(j��)ÿ������K164�����ϵ��˔�(sh��)���Y(ji��)���������뵽����(sh��)����
��ii������ȫ�꼉���ЌW(xu��)�����S�C(j��)��ȡ3�ˣ�ÿ������K��179�����ϵ��˔�(sh��)��![]() �����S�C(j��)׃��
�����S�C(j��)׃��![]() �ķֲ��к͔�(sh��)�W(xu��)�����c����.
�ķֲ��к͔�(sh��)�W(xu��)�����c����.
�������S�C(j��)׃��![]() �������B(t��i)�ֲ�
�������B(t��i)�ֲ�![]() ���t
���t![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У�����![]() ���Ƀɂ����c(di��n)
���Ƀɂ����c(di��n)![]() ���c(di��n)
���c(di��n)![]() �ľ��x֮�e����
�ľ��x֮�e����![]() �������c(di��n)�M�ɵģ���������
�������c(di��n)�M�ɵģ���������![]() ���������Ă��Y(ji��)Փ��������
���������Ă��Y(ji��)Փ��������![]() ���S���Q�D�Σ�������
���S���Q�D�Σ�������![]() �����е��c(di��n)���چ�λ�A
�����е��c(di��n)���چ�λ�A![]() ��(n��i)��������
��(n��i)��������![]() �����Č��Q�D�Σ�������
�����Č��Q�D�Σ�������![]() �������c(di��n)�Ŀv����(bi��o)
�������c(di��n)�Ŀv����(bi��o)![]() .���У��������_�Y(ji��)Փ����̖��______.
.���У��������_�Y(ji��)Փ����̖��______.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ������c(di��n)��
������c(di��n)��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ���x���ʞ�
���x���ʞ�![]() ��
��![]() �ǙE�A�ϵ�һ�����c(di��n)�����c������c(di��n)�غϣ�����
�ǙE�A�ϵ�һ�����c(di��n)�����c������c(di��n)�غϣ�����![]() �����L��6���c(di��n)
�����L��6���c(di��n)![]() �P(gu��n)��ԭ�c(di��n)�Č��Q�c(di��n)��
�P(gu��n)��ԭ�c(di��n)�Č��Q�c(di��n)��![]() ��ֱ��
��ֱ��![]() �����c(di��n)
�����c(di��n)![]() .
.
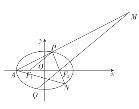
��1����E�A���̣�
��2����ֱ��![]() �c�E�A������һ�c(di��n)
�c�E�A������һ�c(di��n)![]() ����
����![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o).
������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ����ֵ��
�ϵ����ֵ��
��2�����^�c(di��n)![]() ����3�lֱ���c����
����3�lֱ���c����![]() ���У���
���У���![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�����
�У�����![]() �������Σ�
�������Σ�![]() ƽ��
ƽ��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �քe��
�քe��![]() �����c(di��n).
�����c(di��n).
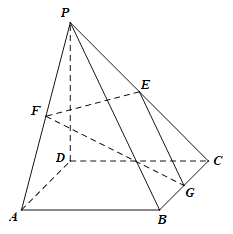
�������C��![]() ��
��
�������C��![]()
![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() �cƽ��
�cƽ��![]() ���ɶ����
���ɶ����![]() ���J�ǣ�������ֵ.
���J�ǣ�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() (a>b>0)�����ҽ��c(di��n)�քe��F1,F2,������2c,��ֱ��y=
(a>b>0)�����ҽ��c(di��n)�քe��F1,F2,������2c,��ֱ��y=![]() (x+c)�c�E�A����M�c(di��n),�ҝM����MF1F2=2��MF2F1,�t�E�A���x������ ( )
(x+c)�c�E�A����M�c(di��n),�ҝM����MF1F2=2��MF2F1,�t�E�A���x������ ( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1��������![]() ������
������![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2��������![]() ��ʹ
��ʹ![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3��������![]() ������
������![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com