
【題目】已知等差數(shù)列![]() 的公差d>0,則下列四個(gè)命題:
的公差d>0,則下列四個(gè)命題:
①數(shù)列![]() 是遞增數(shù)列; ②數(shù)列
是遞增數(shù)列; ②數(shù)列![]() 是遞增數(shù)列;
是遞增數(shù)列;
③數(shù)列![]() 是遞增數(shù)列; ④數(shù)列
是遞增數(shù)列; ④數(shù)列![]() 是遞增數(shù)列.
是遞增數(shù)列.
其中正確命題的個(gè)數(shù)為( )
A.1B.2C.3D.4
【答案】B
【解析】
根據(jù)等差數(shù)列的通項(xiàng)公式和前![]() 項(xiàng)和公式,結(jié)合數(shù)列的通項(xiàng)公式的函數(shù)性質(zhì)進(jìn)行求解即可.
項(xiàng)和公式,結(jié)合數(shù)列的通項(xiàng)公式的函數(shù)性質(zhì)進(jìn)行求解即可.
①:因?yàn)閿?shù)列![]() 是等差數(shù)列,
是等差數(shù)列,
所以![]() ,
,
因此可以把![]() 看成關(guān)于
看成關(guān)于![]() 的一次函數(shù),
的一次函數(shù),
而![]() ,所以數(shù)列
,所以數(shù)列![]() 是遞增數(shù)列,因此本命題是真命題;
是遞增數(shù)列,因此本命題是真命題;
②:因?yàn)閿?shù)列![]() 是等差數(shù)列,
是等差數(shù)列,
所以![]() ,
,
因此可以把![]() 看成關(guān)于
看成關(guān)于![]() 的二次函數(shù),而二次函數(shù)的單調(diào)性與開(kāi)口和對(duì)稱軸有關(guān),
的二次函數(shù),而二次函數(shù)的單調(diào)性與開(kāi)口和對(duì)稱軸有關(guān),
雖然![]() 能確定開(kāi)口方向,但是不能確定對(duì)稱軸的位置,故不能判斷數(shù)列
能確定開(kāi)口方向,但是不能確定對(duì)稱軸的位置,故不能判斷數(shù)列![]() 的單調(diào)性,故本命題是假命題;
的單調(diào)性,故本命題是假命題;
③:因?yàn)閿?shù)列![]() 是等差數(shù)列,
是等差數(shù)列,
所以![]() ,
,
設(shè)![]() ,因此數(shù)列
,因此數(shù)列![]() 的通項(xiàng)公式為:
的通項(xiàng)公式為:![]() ,
,
顯然當(dāng)![]() 時(shí),數(shù)列
時(shí),數(shù)列![]() 是常數(shù)列,故本命題是假命題;
是常數(shù)列,故本命題是假命題;
④:因?yàn)閿?shù)列![]() 是等差數(shù)列,
是等差數(shù)列,
所以![]() ,
,
設(shè)![]() ,因此數(shù)列
,因此數(shù)列![]() 的通項(xiàng)公式為
的通項(xiàng)公式為![]() ,
,
所以可以把![]() 看成關(guān)于
看成關(guān)于![]() 的一次函數(shù),
的一次函數(shù),
而![]() ,所以數(shù)列
,所以數(shù)列![]() 是遞增數(shù)列,因此本命題是真命題.
是遞增數(shù)列,因此本命題是真命題.
故選:B



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖, ![]() 是邊長(zhǎng)為
是邊長(zhǎng)為![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.
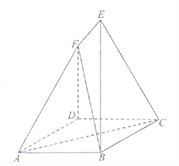
(Ⅰ)求證: ![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地區(qū)高考實(shí)行新方案,規(guī)定:語(yǔ)文、數(shù)學(xué)和英語(yǔ)是考生的必考科目,考生還須從物理、化學(xué)、生物、歷史、地理和政治六個(gè)科目中選取三個(gè)科目作為選考科目.若一個(gè)學(xué)生從六個(gè)科目中選出了三個(gè)科目作為選考科目,則稱該學(xué)生的選考方案確定;否則,稱該學(xué)生選考方案待確定.例如,學(xué)生甲選擇“物理、化學(xué)和生物”三個(gè)選考科目,則學(xué)生甲的選考方案確定,“物理、化學(xué)和生物”為其選考方案.
某學(xué)校為了解高一年級(jí)420名學(xué)生選考科目的意向,隨機(jī)選取30名學(xué)生進(jìn)行了一次調(diào)查,統(tǒng)計(jì)選考科目人數(shù)如下表: