
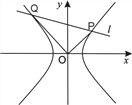
【題目】已知雙曲線![]() (b>a>0),O為坐標原點,離心率
(b>a>0),O為坐標原點,離心率![]() ,點
,點![]() 在雙曲線上.
在雙曲線上.
(1)求雙曲線的方程;
(2)若直線![]() 與雙曲線交于P、Q兩點,且
與雙曲線交于P、Q兩點,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
【答案】![]() 1
1![]()
![]() ;
;![]() 2
2![]() .
.
【解析】試題分析:
(Ⅰ) 由![]() ,可得
,可得![]() ,故雙曲線方程為
,故雙曲線方程為![]() ,代入點
,代入點![]() 的坐標可得
的坐標可得![]() ,由此可得雙曲線方程. (Ⅱ)根據(jù)直線
,由此可得雙曲線方程. (Ⅱ)根據(jù)直線![]() 的斜率存在與否分兩種情況求解.當斜率存在時,可根據(jù)一元二次方程根與系數(shù)的關(guān)系及兩點間的距離公式求解即可.當斜率不存在時直接計算可得結(jié)果.
的斜率存在與否分兩種情況求解.當斜率存在時,可根據(jù)一元二次方程根與系數(shù)的關(guān)系及兩點間的距離公式求解即可.當斜率不存在時直接計算可得結(jié)果.
試題解析:
(1)由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴ 雙曲線方程為![]() ,
,
∵ 點![]() 在雙曲線上,
在雙曲線上,
∴![]() ,
,
解得 ![]() ,
,
∴ 雙曲線的方程為![]() .
.
(2)①當直線![]() 的斜率存在時,設(shè)直線
的斜率存在時,設(shè)直線![]() 的方程為
的方程為![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直線![]() 與雙曲線交于
與雙曲線交于![]() 兩點,
兩點,
∴![]() .
.
設(shè)![]() ,
,![]() ,
,
則![]() ,
,
由![]() 得到:
得到:![]() ,
,
即![]() ,
,
∴![]() ,
,
化簡得![]() .
.
∴![]() ,
,
當![]() 時上式取等號,且方程(*)有解.
時上式取等號,且方程(*)有解.
②當直線![]() 的斜率不存在時,設(shè)直線
的斜率不存在時,設(shè)直線![]() 的方程為
的方程為![]() ,則有
,則有![]() ,
,
由![]() 可得
可得![]() ,
,
可得![]() ,解得
,解得![]() .
.
∴![]() .
.
∴![]()
![]() .
.
綜上可得![]() 的最小值是24.
的最小值是24.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=1,|an+1﹣an|=pn , n∈N* .
(1)若{an}是遞增數(shù)列,且a1 , 2a2 , 3a3成等差數(shù)列,求p的值;
(2)若p= ![]() ,且{a2n﹣1}是遞增數(shù)列,{a2n}是遞減數(shù)列,求數(shù)列{an}的通項公式.
,且{a2n﹣1}是遞增數(shù)列,{a2n}是遞減數(shù)列,求數(shù)列{an}的通項公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)空氣質(zhì)量指數(shù)API(為整數(shù))的不同,可將空氣質(zhì)量分級如下表:
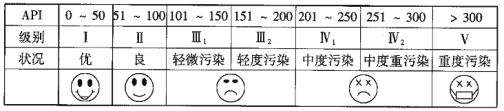
對某城市一年(365天)的空氣質(zhì)量進行監(jiān)測,獲得的API數(shù)據(jù)按照區(qū)間![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,得到頻率分布條形圖如圖.
進行分組,得到頻率分布條形圖如圖.
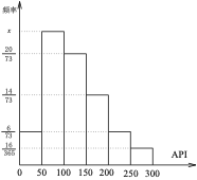
(1)求圖中![]() 的值;
的值;
(2)空氣質(zhì)量狀況分別為輕微污染或輕度污染定為空氣質(zhì)量Ⅲ級,求一年中空氣質(zhì)量為Ⅲ級的天數(shù)
(3)小張到該城市出差一天,這天空氣質(zhì)量為優(yōu)良的概率是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() 上一個動點,
上一個動點, ![]() 為圓
為圓![]() 上一個動點,那么點
上一個動點,那么點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到拋物線的準線距離之和的最小值是( )
到拋物線的準線距離之和的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)有小學(xué)21所,中學(xué)14所,大學(xué)7所,現(xiàn)采取分層抽樣的方法從這些學(xué)校中抽取6所學(xué)校對學(xué)生進行視力調(diào)查。
(I)求應(yīng)從小學(xué)、中學(xué)、大學(xué)中分別抽取的學(xué)校數(shù)目。
(II)若從抽取的6所學(xué)校中隨機抽取2所學(xué)校做進一步數(shù)據(jù)分析,
(1)列出所有可能的抽取結(jié)果;
(2)求抽取的2所學(xué)校均為小學(xué)的概率。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若等比數(shù)列{an}的各項均為正數(shù),且a10a11+a9a12=2e5 , 則lna1+lna2+…lna20= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
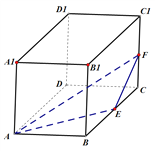
【題目】如圖,在棱長為1的正方體![]() 中,點
中,點![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,
的中點,![]() 是側(cè)面
是側(cè)面![]() 內(nèi)一點,若
內(nèi)一點,若![]()
![]() 平面
平面![]() ,則線段
,則線段![]() 長度的取值范圍是( )
長度的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)![]() ,若存在
,若存在![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 的不動點.已知函數(shù)
的不動點.已知函數(shù)![]()
![]() .
.
(1)當![]() ,
,![]() 時,求函數(shù)
時,求函數(shù)![]() 的不動點;
的不動點;
(2)若對任意實數(shù)![]() ,函數(shù)
,函數(shù)![]() 恒有兩個相異的不動點,求
恒有兩個相異的不動點,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若![]() 的兩個不動點為
的兩個不動點為![]() ,
,![]() ,且
,且![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com