
(本小題滿分14分)給定函數(shù)
(1)試求函數(shù) 的單調(diào)減區(qū)間;
的單調(diào)減區(qū)間;
(2)已知各項均為負的數(shù)列 滿足,
滿足, 求證:
求證: ;
;
(3)設(shè) ,
, 為數(shù)列
為數(shù)列 的前
的前 項和,求證:
項和,求證: 。
。
(1)  的定義域為
的定義域為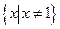 ………1分 (此處不寫定義域,結(jié)果正確不扣分)
………1分 (此處不寫定義域,結(jié)果正確不扣分) 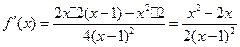 …………3分
…………3分
由 得
得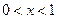 或
或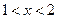
單調(diào)減區(qū)間為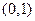 和
和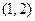 ………5分(答案寫成(0,2)扣1分;不寫區(qū)間形式扣1分)
………5分(答案寫成(0,2)扣1分;不寫區(qū)間形式扣1分)
(2)由已知可得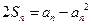 , 當
, 當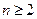 時,
時,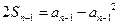
兩式相減得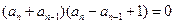
∴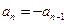 或
或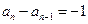
當 時,
時,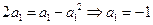 ,若
,若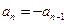 ,則
,則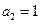 這與題設(shè)矛盾
這與題設(shè)矛盾
∴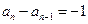 ∴
∴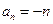 ……8分
……8分
于是,待證不等式即為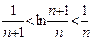 。
。
為此,我們考慮證明不等式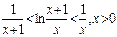
令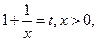 則
則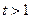 ,
,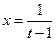
再令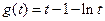 ,
,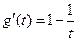 由
由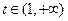 知
知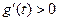
∴當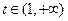 時,
時,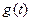 單調(diào)遞增 ∴
單調(diào)遞增 ∴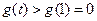 于是
于是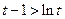
即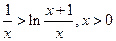 ①
①
令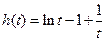 ,
,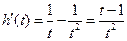 由
由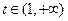 知
知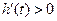
∴當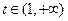 時,
時,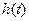 單調(diào)遞增 ∴
單調(diào)遞增 ∴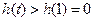
 于是
于是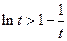
即 ②
②
由①、②可知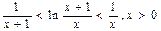 ………………10分
………………10分
所以,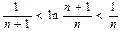 ,即
,即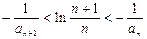 ………………11分
………………11分
(3)由(2)可知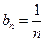 則
則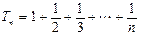 ……12分
……12分
在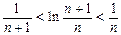 中令n=1,2,3…………..2010,2011并將各式相加得
中令n=1,2,3…………..2010,2011并將各式相加得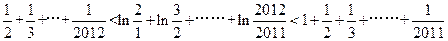 ……13分
……13分
即  ………………14分
………………14分
解析


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
 .
.
(1)討論函數(shù) 在定義域內(nèi)的極值點的個數(shù);
在定義域內(nèi)的極值點的個數(shù);
(2)若函數(shù) 在
在 處取得極值,對
處取得極值,對
 ,
, 恒成立,
恒成立,
求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分) 設(shè)函數(shù)f (x)=ln x+ 在(0,
在(0,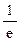 ) 內(nèi)有極值.
) 內(nèi)有極值.
(Ⅰ) 求實數(shù)a的取值范圍;
(Ⅱ) 若x1∈(0,1),x2∈(1,+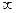 ).求證:f (x2)-f (x1)>e+2-
).求證:f (x2)-f (x1)>e+2-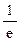 .
.
注:e是自然對數(shù)的底數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)一艘輪船在航行中的燃料費和它的速度的立方成正比,已知在速度為每小時10公里時的燃料費是每小時6元,而其他與速度無關(guān)的費用是每小時96元,問此輪船以何種速度航行時,能使行駛每公里的費用總和最小?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)
已知函數(shù) ,
, ,
,
(Ⅰ)當 時,若
時,若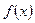 在
在 上單調(diào)遞增,求
上單調(diào)遞增,求 的取值范圍;
的取值范圍;
(Ⅱ)求滿足下列條件的所有實數(shù)對 :當
:當 是整數(shù)時,存在
是整數(shù)時,存在 ,使得
,使得 是
是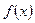 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)對滿足(Ⅱ)的條件的一個實數(shù)對 ,試構(gòu)造一個定義在
,試構(gòu)造一個定義在 ,且
,且 上的函數(shù)
上的函數(shù)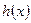 ,使當
,使當 時,
時,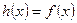 ,當
,當 時,
時,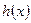 取得最大值的自變量的值構(gòu)成以
取得最大值的自變量的值構(gòu)成以 為首項的等差數(shù)列。
為首項的等差數(shù)列。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知函數(shù)f(x)=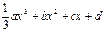 ,其中a , b , c是以d為公差的等差數(shù)列,且a>0,d>0.設(shè)
,其中a , b , c是以d為公差的等差數(shù)列,且a>0,d>0.設(shè)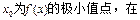 [1-
[1-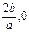 ]上,
]上,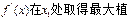 ,在
,在
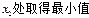 ,將點
,將點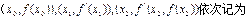 A, B, C,
A, B, C,
(Ⅰ)求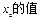
(II)若⊿ABC有一邊平行于x軸,且面積為 ,求a ,d的值.
,求a ,d的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(12分)設(shè)函數(shù)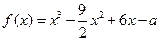 .
.
(1)對于任意實數(shù)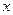 ,
,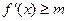 恒成立,求
恒成立,求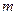 的最大值;
的最大值;
(2)若方程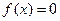 有且僅有一個實根,求
有且僅有一個實根,求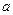 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)已知函數(shù)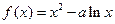 (常數(shù)
(常數(shù)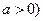 .
.
(Ⅰ) 當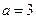 時,求曲線
時,求曲線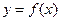 在點
在點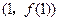 處的切線方程;
處的切線方程;
(Ⅱ)討論函數(shù)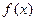 在區(qū)間
在區(qū)間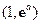 上零點的個數(shù)(
上零點的個數(shù)(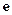 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com