【題目】設(shè)點(diǎn)
為坐標(biāo)原點(diǎn)，橢圓
：
的右頂點(diǎn)為
，上頂點(diǎn)為
，過點(diǎn)且斜率為
的直線與直線
相交于點(diǎn)
，且
.
（1）求橢圓的離心率
；
（2）
是圓
：
的一條直徑，若橢圓經(jīng)過
，
兩點(diǎn)，求橢圓的方程.
【答案】(1) 
.
（2）
.
【解析】分析：（1）運(yùn)用向量的坐標(biāo)運(yùn)算，可得M的坐標(biāo)，進(jìn)而得到直線OM的斜率，進(jìn)而得證；
（2）由（1）知
，橢圓方程設(shè)為
，設(shè)PQ的方程，與橢圓聯(lián)立，運(yùn)用韋達(dá)定理和中點(diǎn)坐標(biāo)公式，以及弦長公式，解方程即可得到a，b的值，進(jìn)而得到橢圓方程.
詳解：（1）∵
，
，
，所以
.
∴
，解得，
于是
，∴橢圓
的離心率
為.
（2）由（1）知，∴橢圓的方程為
即①
依題意，圓心
是線段
的中點(diǎn)，且
.
由對稱性可知，與
軸不垂直，設(shè)其直線方程為
，代入①得：
，
設(shè)
，
，則
，
，
由
得
，解得
.
于是
.于是
.
解得：
，
，∴橢圓的方程為.
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某地隨著經(jīng)濟(jì)的發(fā)展，居民收入逐年增長，如表是該地一建設(shè)銀行連續(xù)五年的儲蓄存款（年底余額），如表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y（千億元） | 5 | 6 | 7 | 8 | 10 |
為了研究計(jì)算的方便，工作人員將上表的數(shù)據(jù)進(jìn)行了處理，
得到表2：
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（1）求z關(guān)于t的線性回歸方程；
（2）通過（1）中的方程，求出y關(guān)于x的回歸方程；
（3）用所求回歸方程預(yù)測到2010年年底，該地儲蓄存款額可達(dá)多少？
附：對于線性回歸方程
，
其中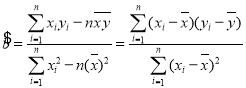
, 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某書店剛剛上市了《中國古代數(shù)學(xué)史》，銷售前該書店擬定了5種單價進(jìn)行試銷，每種單價（
元）試銷l天，得到如表單價（元）與銷量
（冊）數(shù)據(jù)：
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
（l）根據(jù)表中數(shù)據(jù)，請建立關(guān)于的回歸直線方程：
（2）預(yù)計(jì)今后的銷售中，銷量（冊）與單價（元）服從（l）中的回歸方程，已知每冊書的成本是12元，書店為了獲得最大利潤，該冊書的單價應(yīng)定為多少元？
附：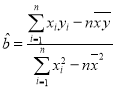
，
，
，
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若一個人下半身長（肚臍至足底）與全身長的比近似為
（
，稱為黃金分割比），堪稱“身材完美”，且比值越接近黃金分割比，身材看起來越好，若某人著裝前測得頭頂至肚臍長度為72
，肚臍至足底長度為103，根據(jù)以上數(shù)據(jù)，作為形象設(shè)計(jì)師的你，對TA的著裝建議是（ ）
A.身材完美，無需改善B.可以戴一頂合適高度的帽子
C.可以穿一雙合適高度的增高鞋D.同時穿戴同樣高度的增高鞋與帽子
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
（1）寫出函數(shù)
的解析式；
（2）若直線
與曲線
有三個不同的交點(diǎn)，求
的取值范圍；
（3）若直線 
與曲線
在
內(nèi)有交點(diǎn)，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從高三抽出
名學(xué)生參加數(shù)學(xué)競賽，由成績得到如下的頻率分布直方圖.試?yán)妙l率分布直方圖求：
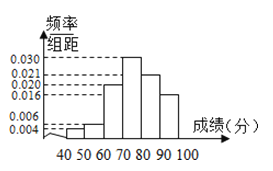
（1）這名學(xué)生成績的眾數(shù)與中位數(shù)；
（2）這名學(xué)生的平均成績.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)甲、乙、丙三個乒乓球協(xié)會分別選派3，1，2名運(yùn)動員參加某次比賽，甲協(xié)會運(yùn)動員編號分別為
，
，
，乙協(xié)會編號為
，丙協(xié)會編號分別為
，
，若從這6名運(yùn)動員中隨機(jī)抽取2名參加雙打比賽.
（1）用所給編號列出所有可能抽取的結(jié)果；
（2）求丙協(xié)會至少有一名運(yùn)動員參加雙打比賽的概率；
（3）求參加雙打比賽的兩名運(yùn)動員來自同一協(xié)會的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列說法中：
①若
，滿足
，則
的最大值為
；
②若
，則函數(shù)
的最小值為
③若，滿足
，則
的最小值為
④函數(shù)
的最小值為
正確的有__________．（把你認(rèn)為正確的序號全部寫上）
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
